Question Number 133568 by bemath last updated on 23/Feb/21
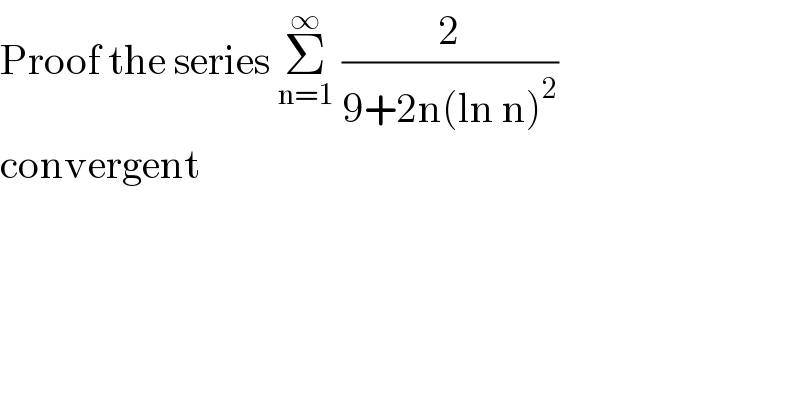
$$\mathrm{Proof}\:\mathrm{the}\:\mathrm{series}\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{2}}{\mathrm{9}+\mathrm{2n}\left(\mathrm{ln}\:\mathrm{n}\right)^{\mathrm{2}} } \\ $$$$\mathrm{convergent} \\ $$$$ \\ $$
Answered by EDWIN88 last updated on 23/Feb/21

$$\:\mathrm{let}\:\mathrm{b}_{\mathrm{n}} =\:\frac{\mathrm{2}}{\mathrm{9}+\mathrm{2n}\:\left(\mathrm{ln}\:\mathrm{n}\right)^{\mathrm{2}} }\:\mathrm{and}\:\mathrm{a}_{\mathrm{n}} \:=\:\frac{\mathrm{2}}{\mathrm{2n}\left(\mathrm{ln}\:\mathrm{n}\right)^{\mathrm{2}} } \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:\frac{\mathrm{2}}{\mathrm{9}+\mathrm{2n}\left(\mathrm{ln}\:\mathrm{n}\right)^{\mathrm{2}} }\:\leqslant\:\frac{\mathrm{2}}{\mathrm{2n}\left(\mathrm{ln}\:\mathrm{n}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{ln}\:\mathrm{n}\right)^{\mathrm{2}} } \\ $$$$\:\mathrm{then}\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{2}}{\mathrm{9}+\mathrm{2n}\left(\mathrm{ln}\:\mathrm{n}\right)^{\mathrm{2}} }\:\leqslant\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{ln}\:\mathrm{n}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$\mathrm{consider}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{ln}\:\mathrm{n}\right)^{\mathrm{2}} }\:=\:\mathrm{0}\:,\:\mathrm{it}\:\mathrm{follows}\:\mathrm{that} \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{ln}\:\mathrm{n}\right)^{\mathrm{2}} }\:\mathrm{convergent}\:,\:\mathrm{then}\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{2}}{\mathrm{9}+\mathrm{2n}\left(\mathrm{ln}\:\mathrm{n}\right)^{\mathrm{2}} } \\ $$$$\mathrm{also}\:\mathrm{convergent} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Answered by mathmax by abdo last updated on 24/Feb/21
![(2/(9+2n(lnn)^2 ))≤(1/(n(ln(n)^2 )) ⇒Σ_(n=1) ^∞ (2/(9+2n(lnn)^2 ))≤Σ_(n=2) ^∞ (1/(n(lnn)^2 )) the serie u_n =(1/(n(lnn)^2 )) is decreazing to o so its nature is same to ∫_2 ^∞ (dx/(x(lnx)^2 )) and changement lnx=t give ∫_2 ^∞ (dx/(x(lnx)^2 ))=∫_(ln2) ^∞ ((e^t dt)/(e^t .t^2 )) =∫_(ln2) ^∞ (dt/t^2 )=[−(1/t)]_(ln2) ^∞ =(1/(ln2))<+∞ ⇒this serie is convergent...!](https://www.tinkutara.com/question/Q133754.png)
$$\frac{\mathrm{2}}{\mathrm{9}+\mathrm{2n}\left(\mathrm{lnn}\right)^{\mathrm{2}} }\leqslant\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{ln}\left(\mathrm{n}\right)^{\mathrm{2}} \right.}\:\Rightarrow\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{2}}{\mathrm{9}+\mathrm{2n}\left(\mathrm{lnn}\right)^{\mathrm{2}} }\leqslant\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{lnn}\right)^{\mathrm{2}} } \\ $$$$\mathrm{the}\:\mathrm{serie}\:\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{lnn}\right)^{\mathrm{2}} }\:\mathrm{is}\:\mathrm{decreazing}\:\mathrm{to}\:\mathrm{o}\:\mathrm{so}\:\mathrm{its}\:\mathrm{nature}\:\mathrm{is}\:\mathrm{same}\:\mathrm{to} \\ $$$$\int_{\mathrm{2}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{lnx}\right)^{\mathrm{2}} }\:\:\mathrm{and}\:\mathrm{changement}\:\mathrm{lnx}=\mathrm{t}\:\mathrm{give} \\ $$$$\int_{\mathrm{2}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{lnx}\right)^{\mathrm{2}} }=\int_{\mathrm{ln2}} ^{\infty} \frac{\mathrm{e}^{\mathrm{t}} \:\mathrm{dt}}{\mathrm{e}^{\mathrm{t}} .\mathrm{t}^{\mathrm{2}} }\:=\int_{\mathrm{ln2}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }=\left[−\frac{\mathrm{1}}{\mathrm{t}}\right]_{\mathrm{ln2}} ^{\infty} =\frac{\mathrm{1}}{\mathrm{ln2}}<+\infty\:\Rightarrow\mathrm{this}\:\mathrm{serie} \\ $$$$\mathrm{is}\:\mathrm{convergent}…! \\ $$
