Menu Close

prove-0-0-2-

Tinku Tara 0 Comments
Pin




Question Number 12332 by frank ntulah last updated on 19/Apr/17
prove ; ((0/0))=2
$$\mathrm{prove}\:;\:\left(\frac{\mathrm{0}}{\mathrm{0}}\right)=\mathrm{2} \\ $$
Commented by FilupS last updated on 20/Apr/17
(0/0)=undefined
$$\frac{\mathrm{0}}{\mathrm{0}}=\mathrm{undefined} \\ $$
Commented by FilupS last updated on 20/Apr/17
lim_(x→0) (x/a)=0 (∣a∣>0) lim_(x→0) (a/x)=±∞ (∣a∣>0) by notation: lim_(L→c) (m/n)=((lim_(L→c) m)/(lim_(L→c) n)) or lim_(L→c) mn=(lim_(L→c) m)(lim_(L→c) n) ∴lim_(x→0) (x/x)=(lim_(x→0) x)(lim_(x→0) (1/x))=0×∞=undefined because: lim_(x→c) (x/x)=1 (∀x≠0) if true for x=0, then 1=0×∞ if 0×∞=0 ⇒ 1=0 if 0×∞=∞ ⇒ 1=∞ both statements make no sense hence (0/0)=undefined Edit: this proof holds true when: (d/dm)m=(d/dn)n=0
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}}{{a}}=\mathrm{0}\:\:\:\:\:\:\left(\mid{a}\mid>\mathrm{0}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{a}}{{x}}=\pm\infty\:\:\:\:\:\:\left(\mid{a}\mid>\mathrm{0}\right) \\ $$$$\: \\ $$$$\mathrm{by}\:\mathrm{notation}: \\ $$$$\underset{{L}\rightarrow{c}} {\mathrm{lim}}\frac{{m}}{{n}}=\frac{\underset{{L}\rightarrow{c}} {\mathrm{lim}}{m}}{\underset{{L}\rightarrow{c}} {\mathrm{lim}}{n}} \\ $$$$\mathrm{or} \\ $$$$\underset{{L}\rightarrow{c}} {\mathrm{lim}}{mn}=\left(\underset{{L}\rightarrow{c}} {\mathrm{lim}}{m}\right)\left(\underset{{L}\rightarrow{c}} {\mathrm{lim}}{n}\right) \\ $$$$ \\ $$$$\therefore\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}}{{x}}=\left(\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{x}\right)\left(\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}\right)=\mathrm{0}×\infty=\mathrm{undefined} \\ $$$$\mathrm{because}: \\ $$$$\underset{{x}\rightarrow{c}} {\mathrm{lim}}\frac{{x}}{{x}}=\mathrm{1}\:\:\:\left(\forall{x}\neq\mathrm{0}\right) \\ $$$$\mathrm{if}\:\mathrm{true}\:\mathrm{for}\:{x}=\mathrm{0},\:\:\mathrm{then}\:\:\:\:\mathrm{1}=\mathrm{0}×\infty \\ $$$$\mathrm{if}\:\:\:\mathrm{0}×\infty=\mathrm{0}\:\:\:\Rightarrow\:\:\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{if}\:\:\:\mathrm{0}×\infty=\infty\:\Rightarrow\:\:\mathrm{1}=\infty \\ $$$$ \\ $$$$\mathrm{both}\:\mathrm{statements}\:\mathrm{make}\:\mathrm{no}\:\mathrm{sense} \\ $$$$\mathrm{hence}\:\frac{\mathrm{0}}{\mathrm{0}}=\mathrm{undefined} \\ $$$$\: \\ $$$$\mathrm{Edit}: \\ $$$$\mathrm{this}\:\mathrm{proof}\:\mathrm{holds}\:\mathrm{true}\:\mathrm{when}:\:\:\frac{{d}}{{dm}}{m}=\frac{{d}}{{dn}}{n}=\mathrm{0} \\ $$
Commented by mrW1 last updated on 20/Apr/17
lim_(x→0) (2sin x)=0 lim_(x→0) (x)=0 but lim_(x→0) ((2sin x)/x)=2
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{2sin}\:{x}\right)=\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left({x}\right)=\mathrm{0} \\ $$$${but}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2sin}\:{x}}{{x}}=\mathrm{2} \\ $$
Commented by FilupS last updated on 20/Apr/17
interesting
$$\mathrm{interesting} \\ $$
Commented by chux last updated on 20/Apr/17
i love this
$$\mathrm{i}\:\mathrm{love}\:\mathrm{this} \\ $$
Commented by geovane10math last updated on 20/Apr/17
((0),(0) ) = 2 ((0!)/(0!(0 − 0)!)) = (1/(1∙1)) = 1 ≠ 2
$$\:\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:=\:\mathrm{2} \\ $$$$\frac{\mathrm{0}!}{\mathrm{0}!\left(\mathrm{0}\:−\:\mathrm{0}\right)!}\:=\:\frac{\mathrm{1}}{\mathrm{1}\centerdot\mathrm{1}}\:=\:\mathrm{1}\:\neq\:\mathrm{2} \\ $$
Commented by FilupS last updated on 20/Apr/17
i added an edit
$$\mathrm{i}\:\mathrm{added}\:\mathrm{an}\:\mathrm{edit} \\ $$
Answered by chux last updated on 20/Apr/17
(0/0)=((100−100)/(100−100))=((10^2 −10^2 )/(10(10−10))) =(((10−10)(10+10))/(10(10−10))) divide common terms =((10+10)/(10))=20/10 =2 note if the nethod is reversed we would have 1/2 that (0/0)=2 is a mathematical falacy
$$\frac{\mathrm{0}}{\mathrm{0}}=\frac{\mathrm{100}−\mathrm{100}}{\mathrm{100}−\mathrm{100}}=\frac{\mathrm{10}^{\mathrm{2}} −\mathrm{10}^{\mathrm{2}} }{\mathrm{10}\left(\mathrm{10}−\mathrm{10}\right)} \\ $$$$=\frac{\left(\mathrm{10}−\mathrm{10}\right)\left(\mathrm{10}+\mathrm{10}\right)}{\mathrm{10}\left(\mathrm{10}−\mathrm{10}\right)} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{divide}\:\mathrm{common}\:\mathrm{terms} \\ $$$$ \\ $$$$=\frac{\mathrm{10}+\mathrm{10}}{\mathrm{10}}=\mathrm{20}/\mathrm{10}\:=\mathrm{2} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{note}\:\mathrm{if}\:\mathrm{the}\:\mathrm{nethod}\:\mathrm{is}\:\mathrm{reversed}\:\mathrm{we}\: \\ $$$$\mathrm{would}\:\mathrm{have}\:\mathrm{1}/\mathrm{2} \\ $$$$ \\ $$$$\mathrm{that}\:\frac{\mathrm{0}}{\mathrm{0}}=\mathrm{2}\:\mathrm{is}\:\mathrm{a}\:\mathrm{mathematical} \\ $$$$\mathrm{falacy} \\ $$
Commented by Joel576 last updated on 20/Apr/17
you cant divide a number by 0
$$\mathrm{you}\:\mathrm{cant}\:\mathrm{divide}\:\mathrm{a}\:\mathrm{number}\:\mathrm{by}\:\mathrm{0} \\ $$
Commented by FilupS last updated on 20/Apr/17
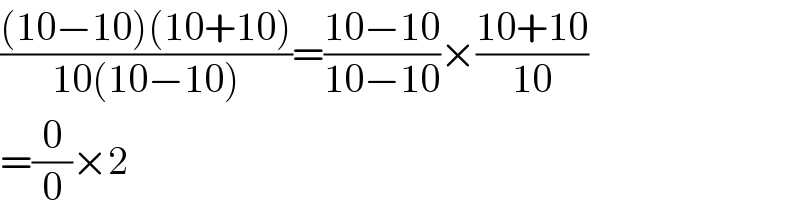
(((10−10)(10+10))/(10(10−10)))=((10−10)/(10−10))×((10+10)/(10)) =(0/0)×2
$$\frac{\left(\mathrm{10}−\mathrm{10}\right)\left(\mathrm{10}+\mathrm{10}\right)}{\mathrm{10}\left(\mathrm{10}−\mathrm{10}\right)}=\frac{\mathrm{10}−\mathrm{10}}{\mathrm{10}−\mathrm{10}}×\frac{\mathrm{10}+\mathrm{10}}{\mathrm{10}} \\ $$$$=\frac{\mathrm{0}}{\mathrm{0}}×\mathrm{2} \\ $$
Commented by chux last updated on 20/Apr/17
thats true.... thanx for the correction.
$$\mathrm{thats}\:\mathrm{true}….\:\mathrm{thanx}\:\mathrm{for}\:\mathrm{the}\:\mathrm{correction}. \\ $$
Commented by frank ntulah last updated on 24/Apr/17
thanks a lot
$$\mathrm{thanks}\:\mathrm{a}\:\mathrm{lot} \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Apr/17
(0/0)=lim_(x→1) ((x^2 −1)/(x−1))=lim_(x→1) (((x+1)(x−1))/(x−1))= lim_(x→1) (x+1)=2 .■ we have a fatal error that dividing by (x−1)that equails to zero in lim.
$$\frac{\mathrm{0}}{\mathrm{0}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}−\mathrm{1}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)}{{x}−\mathrm{1}}= \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left({x}+\mathrm{1}\right)=\mathrm{2}\:\:\:.\blacksquare \\ $$$${we}\:{have}\:{a}\:{fatal}\:{error}\:{that}\:{dividing}\:{by} \\ $$$$\left({x}−\mathrm{1}\right){that}\:{equails}\:{to}\:{zero}\:{in}\:\mathrm{lim}. \\ $$
Commented by FilupS last updated on 21/Apr/17
this is incorrect lim_(x→1) (((x+1)(x−1))/(x−1))≠2 lim_(x→1) (((x+1)(x−1))/(x−1))=lim_(x→1) ((x−1)/(x−1))(x+1) =(0/0)(2)=undefined
$$\mathrm{this}\:\mathrm{is}\:\mathrm{incorrect} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)}{{x}−\mathrm{1}}\neq\mathrm{2} \\ $$$$\: \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)}{{x}−\mathrm{1}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}−\mathrm{1}}{{x}−\mathrm{1}}\left({x}+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{0}}{\mathrm{0}}\left(\mathrm{2}\right)=\mathrm{undefined} \\ $$
Commented by mrW1 last updated on 21/Apr/17
but it is correct! by limit with x→1 it means x is near 1 but ≠1, and x−1≠0, so you can divide with x−1. lim_(x→1) (((x+1)(x−1))/(x−1))=lim_(x→1) (x+1)=2
$${but}\:{it}\:{is}\:{correct}! \\ $$$${by}\:{limit}\:{with}\:{x}\rightarrow\mathrm{1}\:{it}\:{means}\:{x}\:{is}\:{near}\:\mathrm{1}\:{but}\:\neq\mathrm{1},\:{and}\:{x}−\mathrm{1}\neq\mathrm{0},\: \\ $$$${so}\:{you}\:{can}\:{divide}\:{with}\:{x}−\mathrm{1}. \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)}{{x}−\mathrm{1}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left({x}+\mathrm{1}\right)=\mathrm{2} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *