Menu Close

prove-0-1-ln-1-1-x-x-dx-4-ln-e-2-

Tinku Tara 0 Comments
Pin




Question Number 139851 by mnjuly1970 last updated on 01/May/21
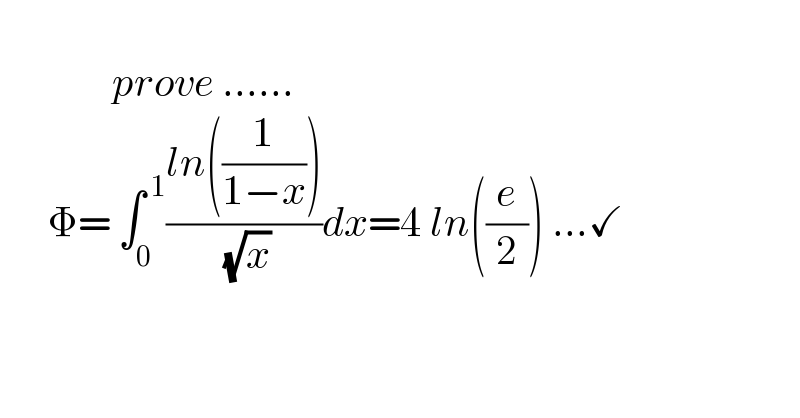
prove ...... Φ= ∫_0 ^( 1) ((ln((1/(1−x))))/( (√x)))dx=4 ln((e/2)) ...✓
$$\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{prove}\:…… \\ $$$$\:\:\:\:\:\:\Phi=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)}{\:\sqrt{{x}}}{dx}=\mathrm{4}\:{ln}\left(\frac{{e}}{\mathrm{2}}\right)\:…\checkmark \\ $$
Answered by mindispower last updated on 01/May/21
Φ=−∫_0 ^1 ((ln(1−x))/( (√x)))⇒Φ=−2∫_0 ^1 ln(1−x).d(√x) =−2∫_0 ^1 ln(1−t^2 )dt=lim_(x→1) [−2tln(1−t^2 )]_0 ^x −4∫_0 ^x (t^2 /(1−t^2 ))=lim_(x→1) −2xln(1−x)+4x−2∫_0 ^x (1/(1−t))+(1/(1+t))dt =lim_(x→1) −2xln(1−x)+2ln(1−x)+4x−2ln(1+x) =lim_(x→1) 2(1−x)ln(1−x)+4−2ln(2) 4ln(e)−4ln(√2)=4ln((e/( (√2))))
$$\Phi=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right)}{\:\sqrt{{x}}}\Rightarrow\Phi=−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{x}\right).{d}\sqrt{{x}} \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{t}^{\mathrm{2}} \right){dt}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left[−\mathrm{2}{tln}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{{x}} \\ $$$$−\mathrm{4}\int_{\mathrm{0}} ^{{x}} \frac{{t}^{\mathrm{2}} }{\mathrm{1}−{t}^{\mathrm{2}} }=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}−\mathrm{2}{xln}\left(\mathrm{1}−{x}\right)+\mathrm{4}{x}−\mathrm{2}\int_{\mathrm{0}} ^{{x}} \frac{\mathrm{1}}{\mathrm{1}−{t}}+\frac{\mathrm{1}}{\mathrm{1}+{t}}{dt} \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}−\mathrm{2}{xln}\left(\mathrm{1}−{x}\right)+\mathrm{2}{ln}\left(\mathrm{1}−{x}\right)+\mathrm{4}{x}−\mathrm{2}{ln}\left(\mathrm{1}+{x}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}2}\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{1}−{x}\right)+\mathrm{4}−\mathrm{2}{ln}\left(\mathrm{2}\right) \\ $$$$\mathrm{4}{ln}\left({e}\right)−\mathrm{4}{ln}\sqrt{\mathrm{2}}=\mathrm{4}{ln}\left(\frac{{e}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$$ \\ $$
Answered by mnjuly1970 last updated on 01/May/21
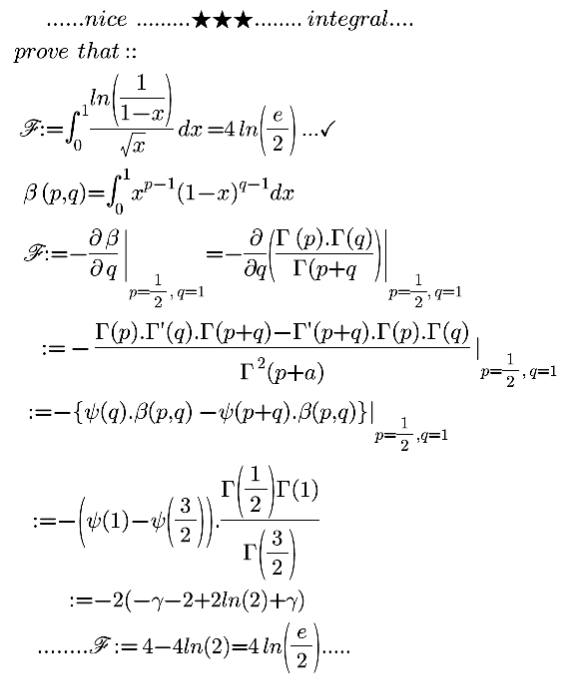
Answered by mnjuly1970 last updated on 01/May/21
solution (2) Φ= ∫_0 ^( 1) Σ_(n=1) ^∞ (x^(n−(1/2)) /n)dx=Σ_(n=1) ^∞ (1/(n(n+(1/2)))) = 2Σ_(n=1) ^∞ ((1/n)−(1/(n+(1/2))))=2(γ−γ+Σ_(n=1) ^∞ (1/n)−(1/(n+(1/2)))) =2γ+2ψ((3/2))=2γ+2(2−γ−2ln(2)) =4−4ln(2)=4ln((e/2)) .....
$$\:\:\:{solution}\:\left(\mathrm{2}\right) \\ $$$$\:\:\:\Phi=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}−\frac{\mathrm{1}}{\mathrm{2}}} }{{n}}{dx}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$\:\:\:=\:\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\frac{\mathrm{1}}{\mathrm{2}}}\right)=\mathrm{2}\left(\gamma−\gamma+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\frac{\mathrm{1}}{\mathrm{2}}}\right) \\ $$$$\:=\mathrm{2}\gamma+\mathrm{2}\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\mathrm{2}\gamma+\mathrm{2}\left(\mathrm{2}−\gamma−\mathrm{2}{ln}\left(\mathrm{2}\right)\right) \\ $$$$=\mathrm{4}−\mathrm{4}{ln}\left(\mathrm{2}\right)=\mathrm{4}{ln}\left(\frac{{e}}{\mathrm{2}}\right)\:….. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *