Prove-by-contradiction-that-there-are-no-whole-number-solutions-x-y-z-to-the-equation-z-2-x-2-y-2-where-both-x-and-y-are-odd-

Question Number 2655 by Yozzi last updated on 24/Nov/15

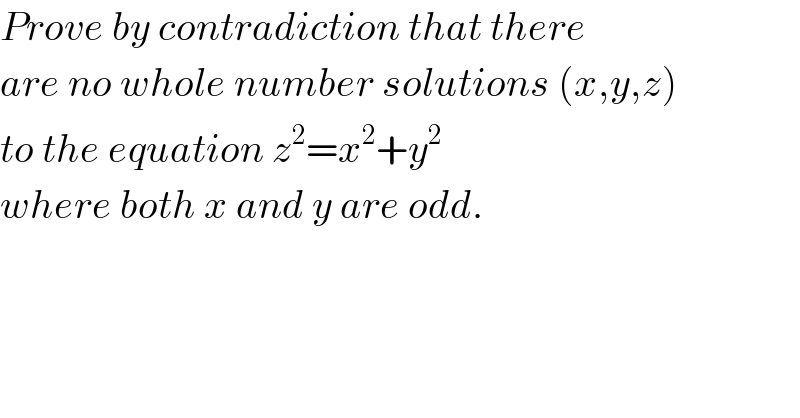
P r o v e b y c o n t r a d i c t i o n t h a t t h e r e

a r e n o w h o l e n u m b e r s o l u t i o n s (x, y, z)

t o t h e e q u a t i o n z^{2} = x^{2} + y^{2}

w h e r e b o t h x a n d y a r e o d d .

Answered by prakash jain last updated on 24/Nov/15

Let us assume that such a solution exists

j, k, l \in N \cup {0}

x = 2 k + 1

y = 2 j + 1

since x, y a r e o d d z m u s t b e e v e n

z = 2 l

z^{2} = x^{2} + y^{2}

4 l^{2} = 4 k^{2} + 4 k + 1 + 4 j^{2} + 4 j + 1

l^{2} = k^{2} + k + j^{2} + j + \frac{1}{2}

l^{2} is a fraction . Contradicts that z is a whole

number or l is a whole number .

Commented by Rasheed Soomro last updated on 24/Nov/15

I n s p i r i n g!

Answered by Filup last updated on 24/Nov/15

z^{2} = x^{2} + y^{2}

z \in Z when :

o d d x = 2 t + 1 t \in Z

o d d y = 2 t + 3 t \in Z

z^{2} = {(2 t + 1)}^{2} + {(2 t + 3)}^{2}

= (4 t^{2} + 2 t + 1 + (4 t^{2} + 6 t + 9))

= (8 t^{2} + 8 t + 10)

= 2 (4 t (t + 1) + 5)

z = \sqrt{2 (4 t (t + 1) + 5)}

= \sqrt{4} \sqrt{2 t (t + 1) + \frac{5}{2}}

z = 2 \sqrt{2 t (t + 1) + \frac{5}{2}} where t \in Z

2 t (t + 1) = whole number

c o n t i n u e ?

Commented by Filup last updated on 24/Nov/15

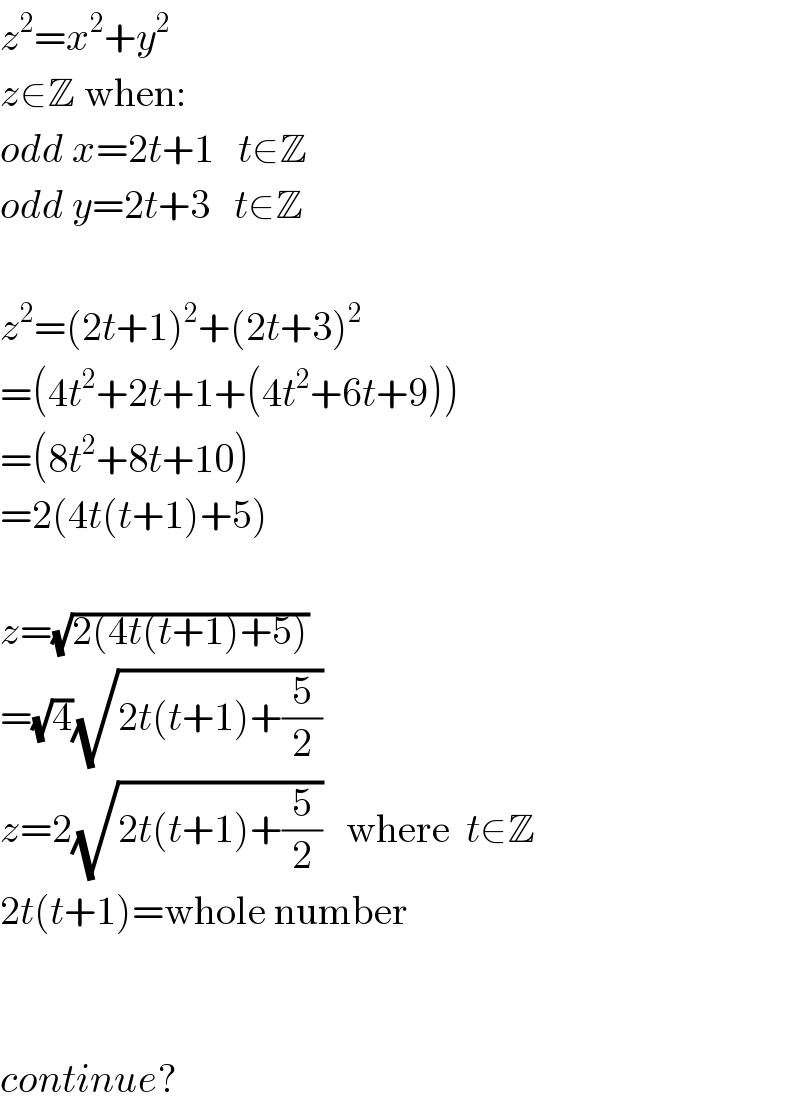
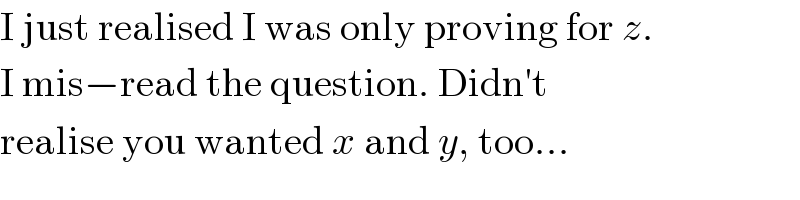
I just realised I was only proving for z .

I mis - read the question . {Didn}^{'} t

realise you wanted x and y, too \dots

Commented by prakash jain last updated on 24/Nov/15

You started with x = 2 t + 1 and y = 2 t + 3

the question only said x and y are odd and

did not state that x and y are consecutive

odd numbers .

The last part of your conclusion

z = 2 \sqrt{2 t (t + 1) + \frac{5}{2}} is valid since you have

a fraction under the root sign so you

cannot get a whole number .

Also proving for z is sufficient as the question

only requires to prove that condition on

all 3 variables are not satisfied simultaneously .

So proving by assuming 2 variables meet

condition and creating a contradiction on

3 rd is sufficient .

Commented by Filup last updated on 24/Nov/15

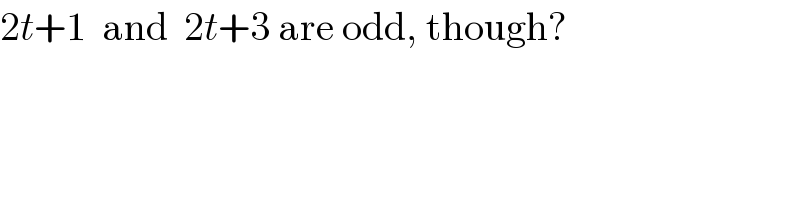
2 t + 1 and 2 t + 3 are odd, though ?

Commented by prakash jain last updated on 24/Nov/15

Yes . But consecutive odd number . So

the conditions are more restrictive than

required by question .

Commented by Filup last updated on 25/Nov/15

I understand now

Facebook Tweet Pin