Prove-by-induction-the-following-result-where-N-is-a-positive-even-integer-S-1-2-S-2-2-2-N-where-S-1-r-1-N-2-1-1-r-1

Question Number 1074 by Yugi last updated on 05/Jun/15

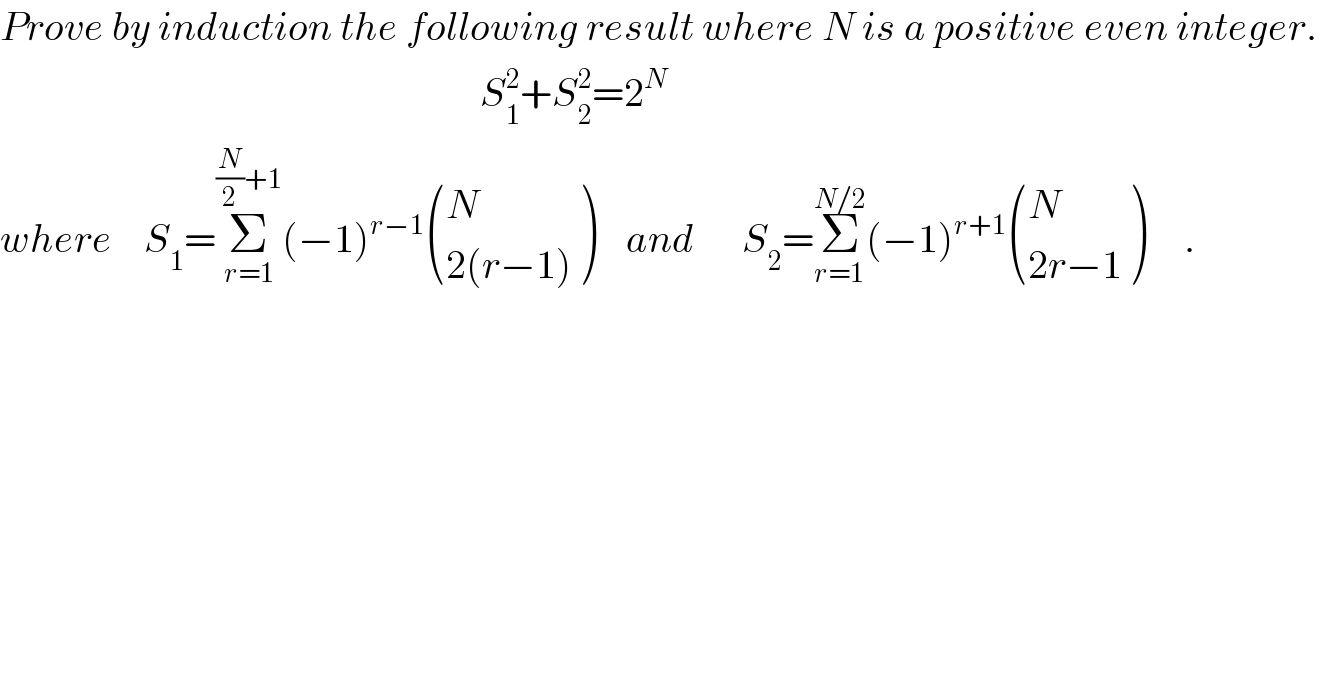
P r o v e b y i n d u c t i o n t h e f o l l o w i n g r e s u l t w h e r e N i s a p o s i t i v e e v e n i n t e g e r .

S_{1}^{2} + S_{2}^{2} = 2^{N}

w h e r e S_{1} = \underset{r = 1}{\sum^{\frac{N}{2} + 1}} {(- 1)}^{r - 1} (\begin{matrix} N \\ 2 (r - 1) \end{matrix}) a n d S_{2} = \underset{r = 1}{\sum^{N / 2}} {(- 1)}^{r + 1} (\begin{matrix} N \\ 2 r - 1 \end{matrix}) .

Commented by prakash jain last updated on 07/Jun/15

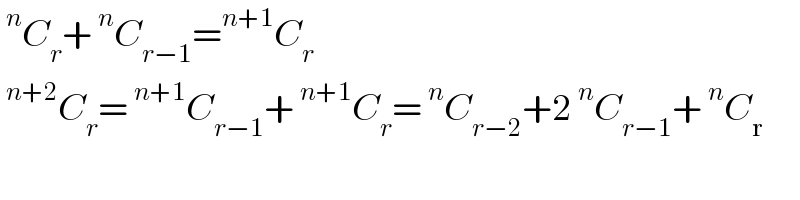
^{n} C_{r} +^{n} C_{r - 1} =^{n + 1} C_{r}

^{n + 2} C_{r} =^{n + 1} C_{r - 1} +^{n + 1} C_{r} =^{n} C_{r - 2} + 2^{n} C_{r - 1} +^{n} C_{r}

Commented by prakash jain last updated on 07/Jun/15

Use the above relation to write {\overset{N + 2}{S}}_{1} in terms

of {\overset{N}{S}}_{1} and {\overset{N}{S}}_{2} .

Commented by 112358 last updated on 07/Jun/15

T h a n k s .

Facebook Tweet Pin