prove-by-mathematical-induction-that-for-all-positive-integers-n-r-1-n-r-r-1-n-3-n-1-n-2-

Question Number 69762 by Rio Michael last updated on 27/Sep/19

p r o v e b y m a t h e m a t i c a l i n d u c t i o n, t h a t f o r a l l p o s i t i v e i n t e g e r s n,

\underset{r = 1}{\sum^{n}} r (r + 1) = \frac{n}{3} (n + 1) (n + 2)

Commented by mathmax by abdo last updated on 27/Sep/19

1 \times 2 + 2 \times 3 + 3 \times 4 + \dots . + n (n + 1) = \frac{n (n + 1) (n + 2)}{3} (★)

n = 1 w e g e t 1 \times 2 = \frac{1 \times 2 \times 3}{3} t h e r e l a t i o n i s t r u e

l e t s u p p o s e (★) t r u e w e h a v e

1 \times 2 + 2 \times 3 + \dots . + (n + 1) (n + 2) = 1 \times 2 + 2 \times 3 + \dots + n (n + 1)

+ (n + 1) (n + 2) = \frac{n (n + 1) (n + 2)}{3} + (n + 1) (n + 2)

= (n + 1) (n + 2) (\frac{n}{3} + 1) = \frac{(n + 1) (n + 2) (n + 3)}{3}

s o t h e r e l s t i o n i s t r u e a t t e r m (n + 1) .

Answered by $@ty@m123 last updated on 27/Sep/19

P (k + 1) :

\underset{r = 1}{\sum^{k + 1}} r (r + 1) = \frac{k}{3} (k + 1) (k + 2) + (k + 1) (k + 2)

= (k + 1) (k + 2) {\frac{k}{3} + 1}

= (k + 1) (k + 2) (\frac{k + 3}{3})

= \frac{k + 1}{3} (k + 2) (k + 3)

\Rightarrow P (k + 1) i s t r u e .

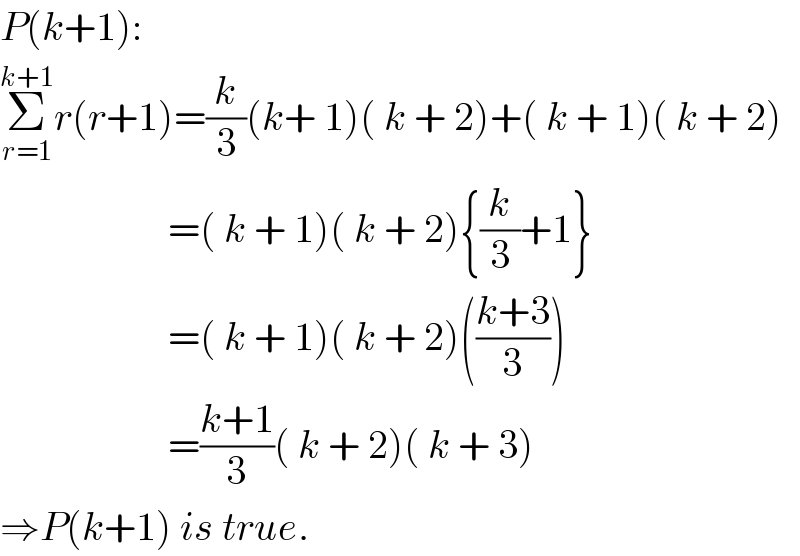
Commented by Rio Michael last updated on 27/Sep/19

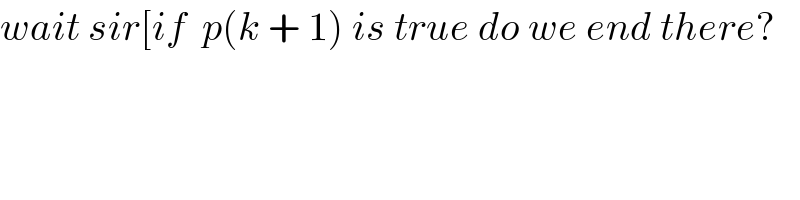
w a i t s i r [i f p (k + 1) i s t r u e d o w e e n d t h e r e ?

Commented by $@ty@m123 last updated on 28/Sep/19

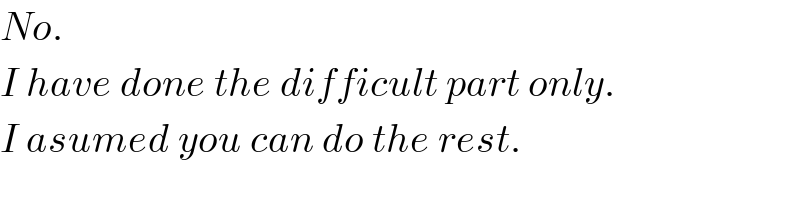
N o .

I h a v e d o n e t h e d i f f i c u l t p a r t o n l y .

I a s u m e d y o u c a n d o t h e r e s t .

Commented by Rio Michael last updated on 28/Sep/19

t h a n k s