Question Number 142729 by mohammad17 last updated on 04/Jun/21
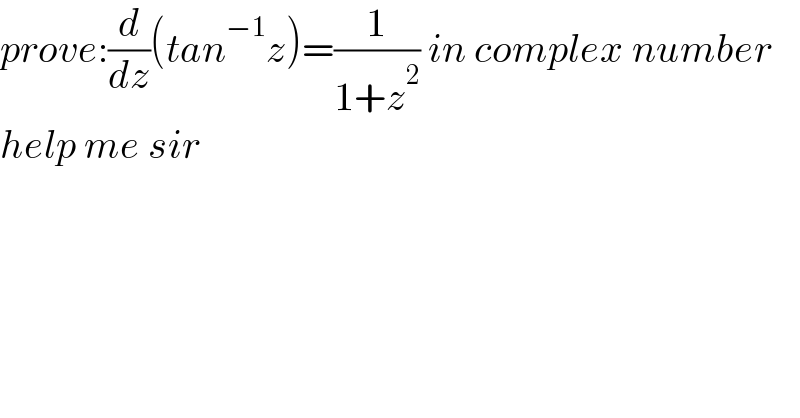
$${prove}:\frac{{d}}{{dz}}\left({tan}^{−\mathrm{1}} {z}\right)=\frac{\mathrm{1}}{\mathrm{1}+{z}^{\mathrm{2}} }\:{in}\:{complex}\:{number} \\ $$$${help}\:{me}\:{sir} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 06/Jun/21
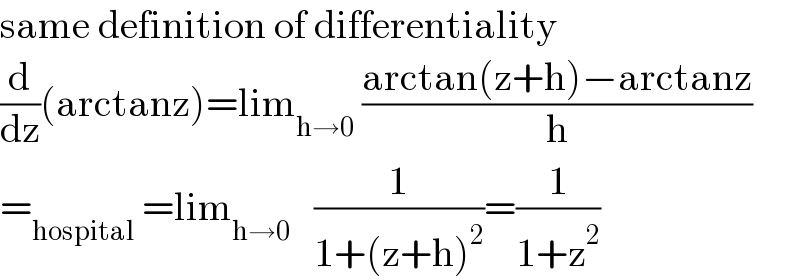
$$\mathrm{same}\:\mathrm{definition}\:\mathrm{of}\:\mathrm{differentiality} \\ $$$$\frac{\mathrm{d}}{\mathrm{dz}}\left(\mathrm{arctanz}\right)=\mathrm{lim}_{\mathrm{h}\rightarrow\mathrm{0}} \:\frac{\mathrm{arctan}\left(\mathrm{z}+\mathrm{h}\right)−\mathrm{arctanz}}{\mathrm{h}} \\ $$$$=_{\mathrm{hospital}} \:=\mathrm{lim}_{\mathrm{h}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+\left(\mathrm{z}+\mathrm{h}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} } \\ $$
