Question Number 4556 by FilupSmith last updated on 07/Feb/16
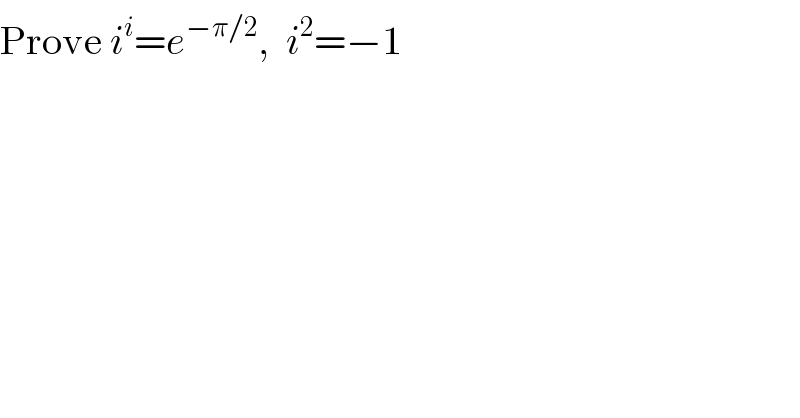
$$\mathrm{Prove}\:{i}^{{i}} ={e}^{−\pi/\mathrm{2}} ,\:\:{i}^{\mathrm{2}} =−\mathrm{1} \\ $$
Answered by Yozzii last updated on 07/Feb/16
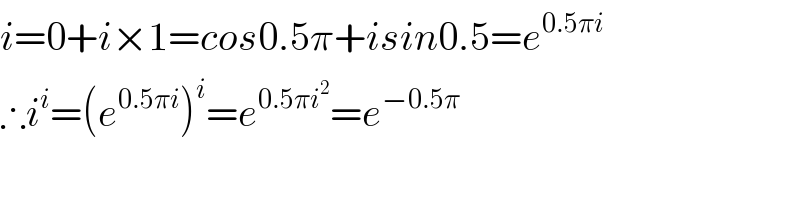
$${i}=\mathrm{0}+{i}×\mathrm{1}={cos}\mathrm{0}.\mathrm{5}\pi+{isin}\mathrm{0}.\mathrm{5}={e}^{\mathrm{0}.\mathrm{5}\pi{i}} \\ $$$$\therefore{i}^{{i}} =\left({e}^{\mathrm{0}.\mathrm{5}\pi{i}} \right)^{{i}} ={e}^{\mathrm{0}.\mathrm{5}\pi{i}^{\mathrm{2}} } ={e}^{−\mathrm{0}.\mathrm{5}\pi} \\ $$
