Menu Close

Prove-k-1-n-n-n-k-k-2-n-1-

Tinku Tara 0 Comments
Pin




Question Number 4092 by Filup last updated on 28/Dec/15
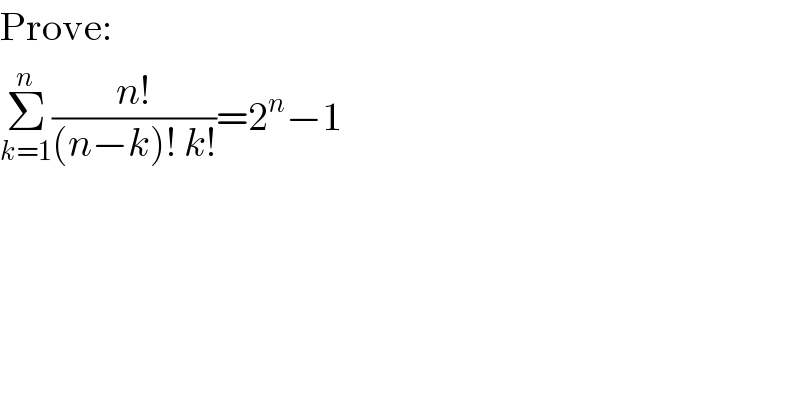
Prove: Σ_(k=1) ^n ((n!)/((n−k)! k!))=2^n −1
$$\mathrm{Prove}: \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{n}!}{\left({n}−{k}\right)!\:{k}!}=\mathrm{2}^{{n}} −\mathrm{1} \\ $$
Answered by Yozzii last updated on 28/Dec/15
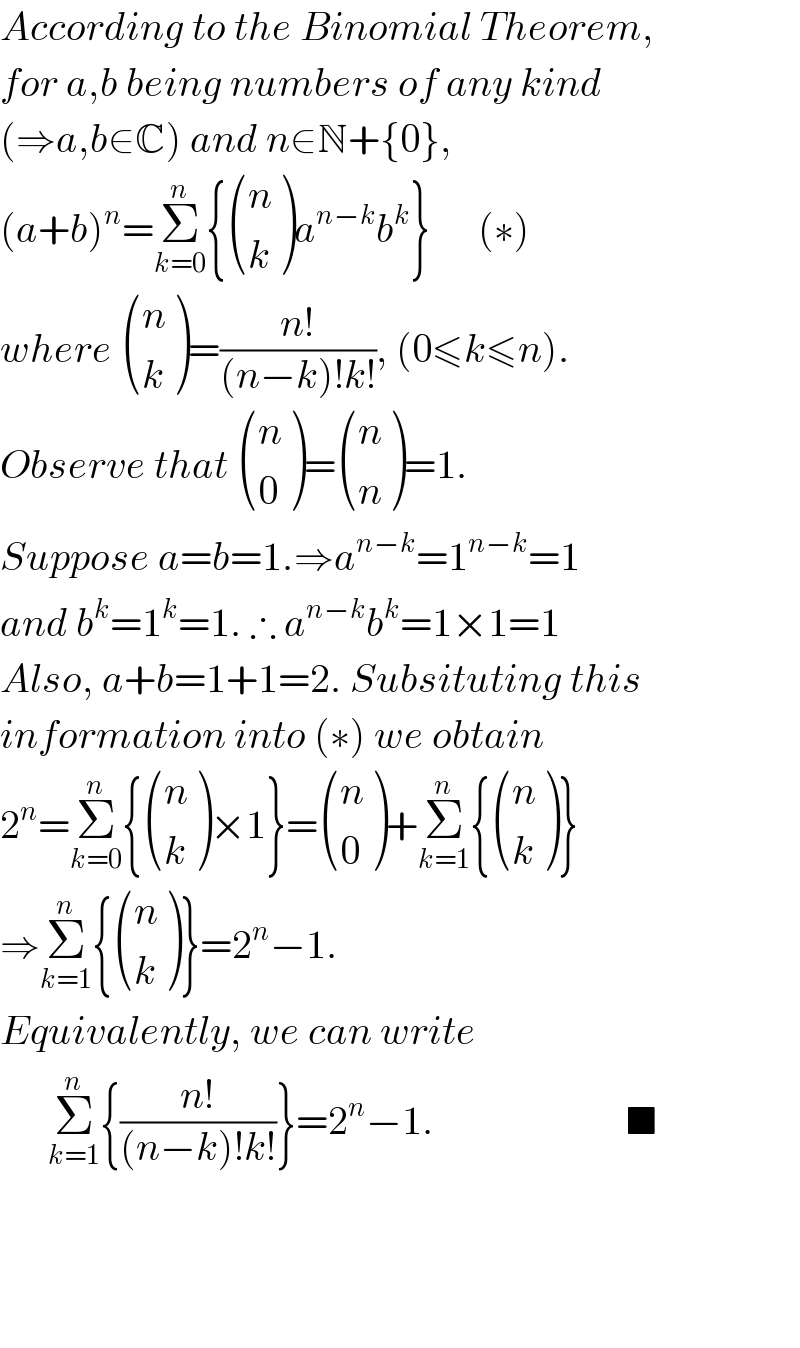
According to the Binomial Theorem, for a,b being numbers of any kind (⇒a,b∈C) and n∈N+{0}, (a+b)^n =Σ_(k=0) ^n { ((n),(k) )a^(n−k) b^k } (∗) where ((n),(k) )=((n!)/((n−k)!k!)), (0≤k≤n). Observe that ((n),(0) )= ((n),(n) )=1. Suppose a=b=1.⇒a^(n−k) =1^(n−k) =1 and b^k =1^k =1. ∴ a^(n−k) b^k =1×1=1 Also, a+b=1+1=2. Subsituting this information into (∗) we obtain 2^n =Σ_(k=0) ^n { ((n),(k) )×1}= ((n),(0) )+Σ_(k=1) ^n { ((n),(k) )} ⇒Σ_(k=1) ^n { ((n),(k) )}=2^n −1. Equivalently, we can write Σ_(k=1) ^n {((n!)/((n−k)!k!))}=2^n −1. ■
$${According}\:{to}\:{the}\:{Binomial}\:{Theorem}, \\ $$$${for}\:{a},{b}\:{being}\:{numbers}\:{of}\:{any}\:{kind} \\ $$$$\left(\Rightarrow{a},{b}\in\mathbb{C}\right)\:{and}\:{n}\in\mathbb{N}+\left\{\mathrm{0}\right\}, \\ $$$$\left({a}+{b}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left\{\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{a}^{{n}−{k}} {b}^{{k}} \right\}\:\:\:\:\:\:\left(\ast\right) \\ $$$${where}\:\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}=\frac{{n}!}{\left({n}−{k}\right)!{k}!},\:\left(\mathrm{0}\leqslant{k}\leqslant{n}\right). \\ $$$${Observe}\:{that}\:\begin{pmatrix}{{n}}\\{\mathrm{0}}\end{pmatrix}=\begin{pmatrix}{{n}}\\{{n}}\end{pmatrix}=\mathrm{1}. \\ $$$${Suppose}\:{a}={b}=\mathrm{1}.\Rightarrow{a}^{{n}−{k}} =\mathrm{1}^{{n}−{k}} =\mathrm{1} \\ $$$${and}\:{b}^{{k}} =\mathrm{1}^{{k}} =\mathrm{1}.\:\therefore\:{a}^{{n}−{k}} {b}^{{k}} =\mathrm{1}×\mathrm{1}=\mathrm{1} \\ $$$${Also},\:{a}+{b}=\mathrm{1}+\mathrm{1}=\mathrm{2}.\:{Subsituting}\:{this} \\ $$$${information}\:{into}\:\left(\ast\right)\:{we}\:{obtain}\: \\ $$$$\mathrm{2}^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left\{\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}×\mathrm{1}\right\}=\begin{pmatrix}{{n}}\\{\mathrm{0}}\end{pmatrix}+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left\{\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\right\} \\ $$$$\Rightarrow\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left\{\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\right\}=\mathrm{2}^{{n}} −\mathrm{1}. \\ $$$${Equivalently},\:{we}\:{can}\:{write} \\ $$$$\:\:\:\:\:\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left\{\frac{{n}!}{\left({n}−{k}\right)!{k}!}\right\}=\mathrm{2}^{{n}} −\mathrm{1}.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\blacksquare \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Yozzii last updated on 28/Dec/15
Proof of Binomial Theorem: Let P(n) be the proposition that,∀n∈N+{0}, (a+b)^n =Σ_(k=0) ^n ((n),(k) )a^(n−k) b^k (∗) where a,b∈C and ((n),(k) )=((n!)/((n−k)!k!)) (0≤k≤n). Let n=0.⇒l.h.s of (∗)=(a+b)^0 =1. r.h.s=Σ_(k=0) ^0 ((0),(k) )a^(0−k) b^k = ((0),(0) )a^(0−0) b^0 = ((0),(0) ) ∵ ((0),(0) )=((0!)/((0−0)!0!))=(1/(0!×1))=(1/1)=1 ⇒r.h.s=1=l.h.s. Hence, P(n) is true when n=0. Assume P(n) is true when n=j (>0) ⇒(a+b)^j =Σ_(k=0) ^j ((j),(k) )a^(j−k) b^k . For n=j+1, (a+b)^(j+1) =(a+b)(a+b)^j =(a+b)(Σ_(k=0) ^j { ((j),(k) )a^(j−k) b^k }) (a+b)^(j+1) =Σ_(k=0) ^j { ((j),(k) )a^(j+1−k) b^k }+bΣ_(k=0) ^j ((j),(k) )a^(j−k) b^k } We acknowledge the following identity for (((j+1)),(k) ). (((j+1)),(k) )= ((j),(k) )+ ((j),((k−1)) ) Proof: The definition of ((n),(k) ) is used. ((j),(k) )+ ((j),((k−1)) )=((j!)/((j−k)!k!))+((j!)/((j−k+1)!(k−1)!)) =((j!)/((j−k)!(k−1)!)){(1/k)+(1/(j−k+1))} =((j!)/((j−k)!(k−1)!))(((j+1−k+k)/(k(j+1−k)))) =((j!(j+1))/((j−k+1)!k!)) =(((j+1)!)/(({j+1}−k)!k!)) = (((j+1)),(k) ) □ Note that ((n),(k) )=0 for k<0 ∴ (a+b)^(j+1) =Σ_(k=0) ^j {( (((j+1)),(k) )− ((j),((k−1)) ))a^(j+1−k) b^k +b(a+b)^n =Σ_(k=0) ^j (((j+1)),(k) )a^(j+1−k) b^k +b(a+b)^j −Σ_(k=0) ^j ((j),((k−1)) )a^(j+1−k) b^k =Σ_(k=0) ^(j+1) { (((j+1)),(k) )a^(j+1−k) b^k }−b^(j+1) +b^(j+1) +Σ_(k=0) ^(j−1) { ((j),(k) )a^(j−k) b^(k+1) }−( ((j),((−1)) )a^(j+1) +Σ_(k=1) ^j { ((j),((k−1)) )a^(j+1−k) b^k }) =Σ_(k=0) ^(j+1) { (((j+1)),(k) )a^(j+1−k) b^k }+0+ ((j),(0) )a^j b− ((j),(0) )a^j + ((j),(1) )a^(j−1) b^2 − ((j),(1) )a^(j−1) b^2 + ((j),(2) )a^(j−2) b^3 − ((j),(2) )a^(j−2) b^3 +...+ ((j),((j−2)) )a^2 b^(j−1) − ((j),((j−2)) )a^2 b^(j−1) + ((j),((j−1)) )ab^j − ((j),((j−1)) )ab^j ⇒(a+b)^(j+1) =Σ_(k=0) ^(j+1) (((j+1)),(k) )a^(j+1−k) b^k Hence,P(j+1) is true,assuming P(j) is true. Since P(0) is true then, by the principle of mathematical induction, P(n) is true ∀n∈N+{0}.
$${Proof}\:{of}\:{Binomial}\:{Theorem}: \\ $$$${Let}\:{P}\left({n}\right)\:{be}\:{the}\:{proposition}\:{that},\forall{n}\in\mathbb{N}+\left\{\mathrm{0}\right\}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\left({a}+{b}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{a}^{{n}−{k}} {b}^{{k}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\ast\right) \\ $$$${where}\:{a},{b}\in\mathbb{C}\:{and}\:\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}=\frac{{n}!}{\left({n}−{k}\right)!{k}!}\:\:\left(\mathrm{0}\leqslant{k}\leqslant{n}\right). \\ $$$${Let}\:{n}=\mathrm{0}.\Rightarrow{l}.{h}.{s}\:{of}\:\left(\ast\right)=\left({a}+{b}\right)^{\mathrm{0}} =\mathrm{1}. \\ $$$${r}.{h}.{s}=\underset{{k}=\mathrm{0}} {\overset{\mathrm{0}} {\sum}}\begin{pmatrix}{\mathrm{0}}\\{{k}}\end{pmatrix}{a}^{\mathrm{0}−{k}} {b}^{{k}} =\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}{a}^{\mathrm{0}−\mathrm{0}} {b}^{\mathrm{0}} =\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\because\:\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}=\frac{\mathrm{0}!}{\left(\mathrm{0}−\mathrm{0}\right)!\mathrm{0}!}=\frac{\mathrm{1}}{\mathrm{0}!×\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{1}}=\mathrm{1} \\ $$$$\Rightarrow{r}.{h}.{s}=\mathrm{1}={l}.{h}.{s}. \\ $$$${Hence},\:{P}\left({n}\right)\:{is}\:{true}\:{when}\:{n}=\mathrm{0}. \\ $$$${Assume}\:{P}\left({n}\right)\:{is}\:{true}\:{when}\:{n}={j}\:\left(>\mathrm{0}\right) \\ $$$$\Rightarrow\left({a}+{b}\right)^{{j}} =\underset{{k}=\mathrm{0}} {\overset{{j}} {\sum}}\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}{a}^{{j}−{k}} {b}^{{k}} . \\ $$$${For}\:{n}={j}+\mathrm{1}, \\ $$$$\left({a}+{b}\right)^{{j}+\mathrm{1}} =\left({a}+{b}\right)\left({a}+{b}\right)^{{j}} =\left({a}+{b}\right)\left(\underset{{k}=\mathrm{0}} {\overset{{j}} {\sum}}\left\{\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}{a}^{{j}−{k}} {b}^{{k}} \right\}\right) \\ $$$$\left.\left({a}+{b}\right)^{{j}+\mathrm{1}} =\underset{{k}=\mathrm{0}} {\overset{{j}} {\sum}}\left\{\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}{a}^{{j}+\mathrm{1}−{k}} {b}^{{k}} \right\}+{b}\underset{{k}=\mathrm{0}} {\overset{{j}} {\sum}}\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}{a}^{{j}−{k}} {b}^{{k}} \right\} \\ $$$$ \\ $$$${We}\:{acknowledge}\:{the}\:{following}\:{identity} \\ $$$${for}\:\begin{pmatrix}{{j}+\mathrm{1}}\\{{k}}\end{pmatrix}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\begin{pmatrix}{{j}+\mathrm{1}}\\{{k}}\end{pmatrix}=\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}+\begin{pmatrix}{{j}}\\{{k}−\mathrm{1}}\end{pmatrix} \\ $$$${Proof}:\: \\ $$$${The}\:{definition}\:{of}\:\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:{is}\:{used}. \\ $$$$\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}+\begin{pmatrix}{{j}}\\{{k}−\mathrm{1}}\end{pmatrix}=\frac{{j}!}{\left({j}−{k}\right)!{k}!}+\frac{{j}!}{\left({j}−{k}+\mathrm{1}\right)!\left({k}−\mathrm{1}\right)!} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{j}!}{\left({j}−{k}\right)!\left({k}−\mathrm{1}\right)!}\left\{\frac{\mathrm{1}}{{k}}+\frac{\mathrm{1}}{{j}−{k}+\mathrm{1}}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{j}!}{\left({j}−{k}\right)!\left({k}−\mathrm{1}\right)!}\left(\frac{{j}+\mathrm{1}−{k}+{k}}{{k}\left({j}+\mathrm{1}−{k}\right)}\right)\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{j}!\left({j}+\mathrm{1}\right)}{\left({j}−{k}+\mathrm{1}\right)!{k}!} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left({j}+\mathrm{1}\right)!}{\left(\left\{{j}+\mathrm{1}\right\}−{k}\right)!{k}!} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\begin{pmatrix}{{j}+\mathrm{1}}\\{{k}}\end{pmatrix}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Box \\ $$$${Note}\:{that}\:\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}=\mathrm{0}\:{for}\:{k}<\mathrm{0}\: \\ $$$$\therefore\:\left({a}+{b}\right)^{{j}+\mathrm{1}} =\underset{{k}=\mathrm{0}} {\overset{{j}} {\sum}}\left\{\left(\begin{pmatrix}{{j}+\mathrm{1}}\\{{k}}\end{pmatrix}−\begin{pmatrix}{{j}}\\{{k}−\mathrm{1}}\end{pmatrix}\right){a}^{{j}+\mathrm{1}−{k}} {b}^{{k}} +{b}\left({a}+{b}\right)^{{n}} \right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{k}=\mathrm{0}} {\overset{{j}} {\sum}}\begin{pmatrix}{{j}+\mathrm{1}}\\{{k}}\end{pmatrix}{a}^{{j}+\mathrm{1}−{k}} {b}^{{k}} +{b}\left({a}+{b}\right)^{{j}} −\underset{{k}=\mathrm{0}} {\overset{{j}} {\sum}}\begin{pmatrix}{{j}}\\{{k}−\mathrm{1}}\end{pmatrix}{a}^{{j}+\mathrm{1}−{k}} {b}^{{k}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{k}=\mathrm{0}} {\overset{{j}+\mathrm{1}} {\sum}}\left\{\begin{pmatrix}{{j}+\mathrm{1}}\\{{k}}\end{pmatrix}{a}^{{j}+\mathrm{1}−{k}} {b}^{{k}} \right\}−{b}^{{j}+\mathrm{1}} +{b}^{{j}+\mathrm{1}} +\underset{{k}=\mathrm{0}} {\overset{{j}−\mathrm{1}} {\sum}}\left\{\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}{a}^{{j}−{k}} {b}^{{k}+\mathrm{1}} \right\}−\left(\begin{pmatrix}{{j}}\\{−\mathrm{1}}\end{pmatrix}{a}^{{j}+\mathrm{1}} +\underset{{k}=\mathrm{1}} {\overset{{j}} {\sum}}\left\{\begin{pmatrix}{{j}}\\{{k}−\mathrm{1}}\end{pmatrix}{a}^{{j}+\mathrm{1}−{k}} {b}^{{k}} \right\}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{k}=\mathrm{0}} {\overset{{j}+\mathrm{1}} {\sum}}\left\{\begin{pmatrix}{{j}+\mathrm{1}}\\{{k}}\end{pmatrix}{a}^{{j}+\mathrm{1}−{k}} {b}^{{k}} \right\}+\mathrm{0}+\begin{pmatrix}{{j}}\\{\mathrm{0}}\end{pmatrix}{a}^{{j}} {b}−\begin{pmatrix}{{j}}\\{\mathrm{0}}\end{pmatrix}{a}^{{j}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\begin{pmatrix}{{j}}\\{\mathrm{1}}\end{pmatrix}{a}^{{j}−\mathrm{1}} {b}^{\mathrm{2}} −\begin{pmatrix}{{j}}\\{\mathrm{1}}\end{pmatrix}{a}^{{j}−\mathrm{1}} {b}^{\mathrm{2}} +\begin{pmatrix}{{j}}\\{\mathrm{2}}\end{pmatrix}{a}^{{j}−\mathrm{2}} {b}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\begin{pmatrix}{{j}}\\{\mathrm{2}}\end{pmatrix}{a}^{{j}−\mathrm{2}} {b}^{\mathrm{3}} +…+\begin{pmatrix}{{j}}\\{{j}−\mathrm{2}}\end{pmatrix}{a}^{\mathrm{2}} {b}^{{j}−\mathrm{1}} −\begin{pmatrix}{{j}}\\{{j}−\mathrm{2}}\end{pmatrix}{a}^{\mathrm{2}} {b}^{{j}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\begin{pmatrix}{{j}}\\{{j}−\mathrm{1}}\end{pmatrix}{ab}^{{j}} −\begin{pmatrix}{{j}}\\{{j}−\mathrm{1}}\end{pmatrix}{ab}^{{j}} \\ $$$$\Rightarrow\left({a}+{b}\right)^{{j}+\mathrm{1}} =\underset{{k}=\mathrm{0}} {\overset{{j}+\mathrm{1}} {\sum}}\begin{pmatrix}{{j}+\mathrm{1}}\\{{k}}\end{pmatrix}{a}^{{j}+\mathrm{1}−{k}} {b}^{{k}} \\ $$$${Hence},{P}\left({j}+\mathrm{1}\right)\:{is}\:{true},{assuming}\:{P}\left({j}\right) \\ $$$${is}\:{true}.\:{Since}\:{P}\left(\mathrm{0}\right)\:{is}\:{true}\:{then},\:{by}\:{the} \\ $$$${principle}\:{of}\:{mathematical}\:{induction}, \\ $$$${P}\left({n}\right)\:{is}\:{true}\:\forall{n}\in\mathbb{N}+\left\{\mathrm{0}\right\}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *