Question Number 143098 by mnjuly1970 last updated on 10/Jun/21
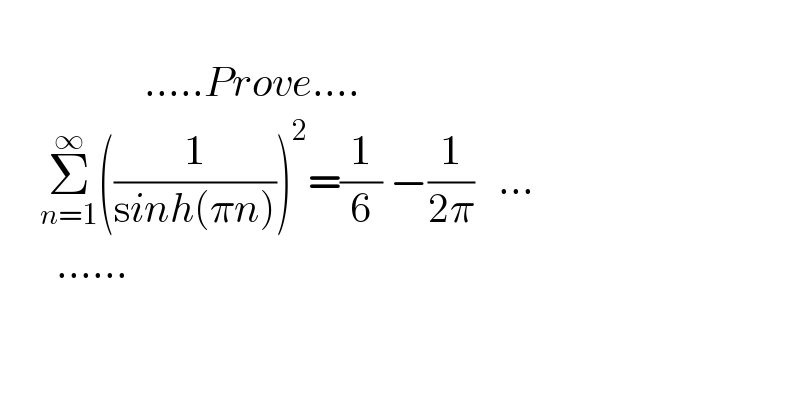
$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…..{Prove}….\: \\ $$$$\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{s}{inh}\left(\pi{n}\right)}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{6}}\:−\frac{\mathrm{1}}{\mathrm{2}\pi}\:\:\:… \\ $$$$\:\:\:\:\:\:\:…… \\ $$
Answered by Dwaipayan Shikari last updated on 10/Jun/21
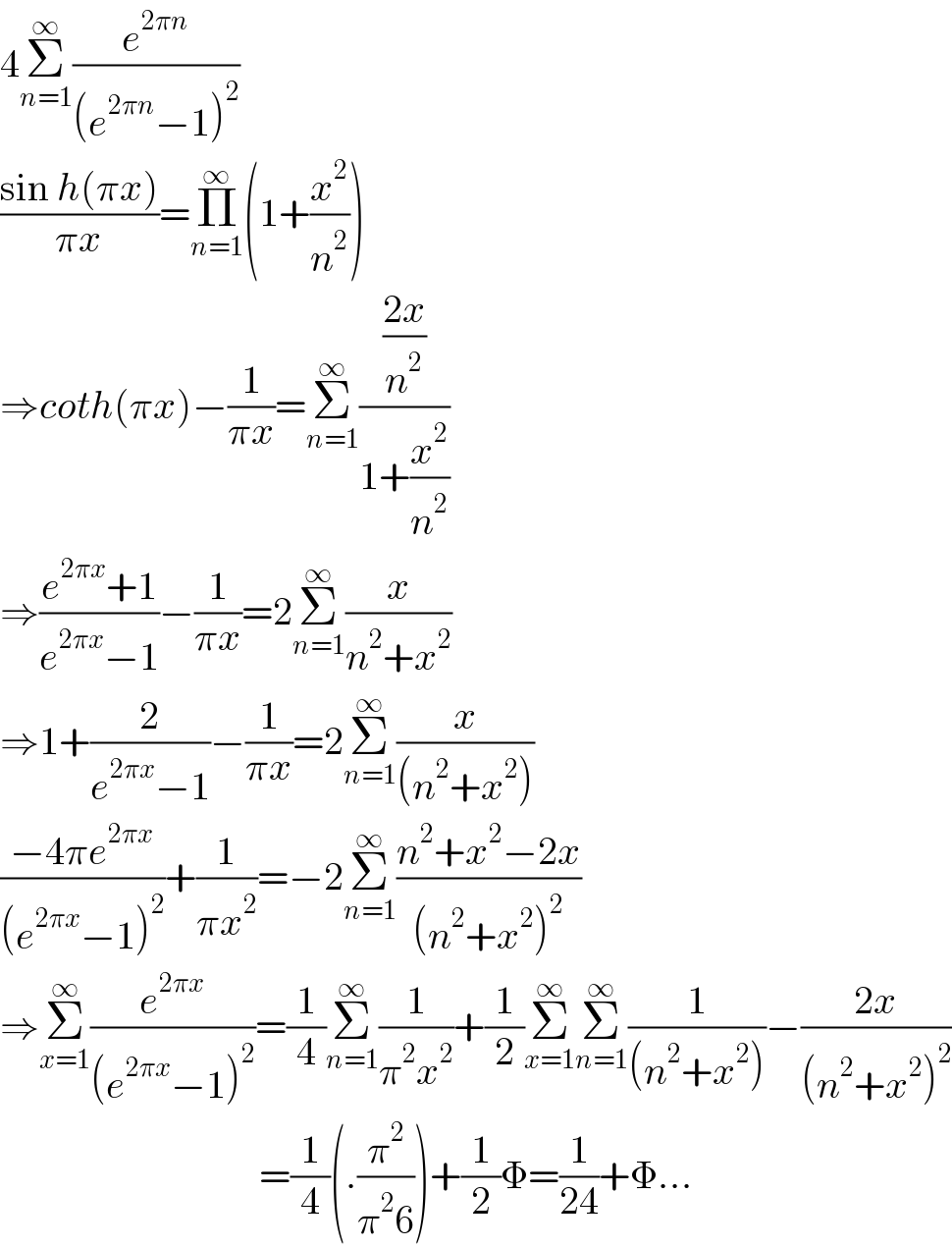
$$\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{\mathrm{2}\pi{n}} }{\left({e}^{\mathrm{2}\pi{n}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{sin}\:{h}\left(\pi{x}\right)}{\pi{x}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{coth}\left(\pi{x}\right)−\frac{\mathrm{1}}{\pi{x}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\frac{\mathrm{2}{x}}{{n}^{\mathrm{2}} }}{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{n}^{\mathrm{2}} }} \\ $$$$\Rightarrow\frac{{e}^{\mathrm{2}\pi{x}} +\mathrm{1}}{{e}^{\mathrm{2}\pi{x}} −\mathrm{1}}−\frac{\mathrm{1}}{\pi{x}}=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}}{{n}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{1}+\frac{\mathrm{2}}{{e}^{\mathrm{2}\pi{x}} −\mathrm{1}}−\frac{\mathrm{1}}{\pi{x}}=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}}{\left({n}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)} \\ $$$$\frac{−\mathrm{4}\pi{e}^{\mathrm{2}\pi{x}} }{\left({e}^{\mathrm{2}\pi{x}} −\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\pi{x}^{\mathrm{2}} }=−\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}{x}}{\left({n}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{\mathrm{2}\pi{x}} }{\left({e}^{\mathrm{2}\pi{x}} −\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\pi^{\mathrm{2}} {x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)}−\frac{\mathrm{2}{x}}{\left({n}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left(.\frac{\pi^{\mathrm{2}} }{\pi^{\mathrm{2}} \mathrm{6}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\Phi=\frac{\mathrm{1}}{\mathrm{24}}+\Phi… \\ $$
Commented by Dwaipayan Shikari last updated on 10/Jun/21

$${Sorry}\:{sir}\:.\:{I}\:\:{have}\:{tried}\: \\ $$
Commented by mnjuly1970 last updated on 10/Jun/21
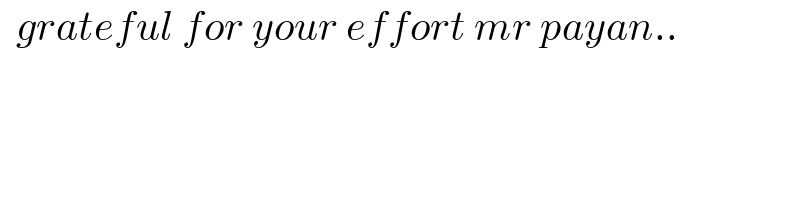
$$\:\:{grateful}\:{for}\:{your}\:{effort}\:{mr}\:{payan}.. \\ $$
