Prove-or-disprove-n-0-1-n-2-97-2-2-97-e-97-e-97-2-388-e-2-97-1-e-2-97-1-37635-37636-1-388-97-

Question Number 131580 by Dwaipayan Shikari last updated on 06/Feb/21

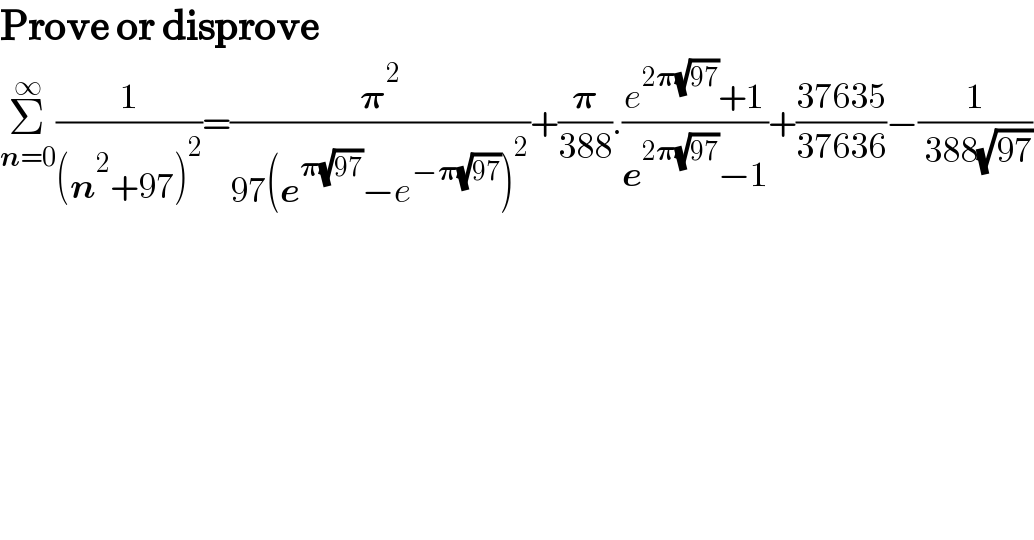
$$\boldsymbol{\mathrm{Prove}}\:\boldsymbol{\mathrm{or}}\:\boldsymbol{\mathrm{disprove}} \\ $$$$\underset{\boldsymbol{{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\boldsymbol{{n}}^{\mathrm{2}} +\mathrm{97}\right)^{\mathrm{2}} }=\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{97}\left(\boldsymbol{{e}}^{\boldsymbol{\pi}\sqrt{\mathrm{97}}} −{e}^{−\boldsymbol{\pi}\sqrt{\mathrm{97}}} \right)^{\mathrm{2}} }+\frac{\boldsymbol{\pi}}{\mathrm{388}}.\frac{{e}^{\mathrm{2}\boldsymbol{\pi}\sqrt{\mathrm{97}}} +\mathrm{1}}{\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{\pi}\sqrt{\mathrm{97}}} −\mathrm{1}}+\frac{\mathrm{37635}}{\mathrm{37636}}−\frac{\mathrm{1}}{\:\mathrm{388}\sqrt{\mathrm{97}}} \\ $$

Commented by Dwaipayan Shikari last updated on 06/Feb/21

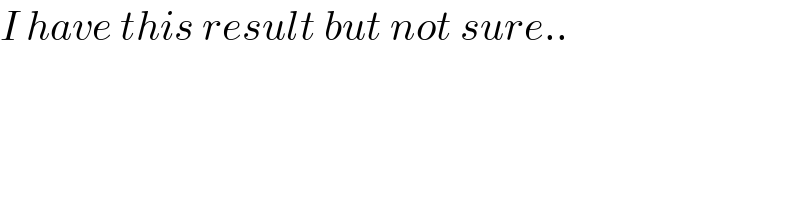
$${I}\:{have}\:{this}\:{result}\:{but}\:{not}\:{sure}.. \\ $$

Commented by mindispower last updated on 09/Feb/21

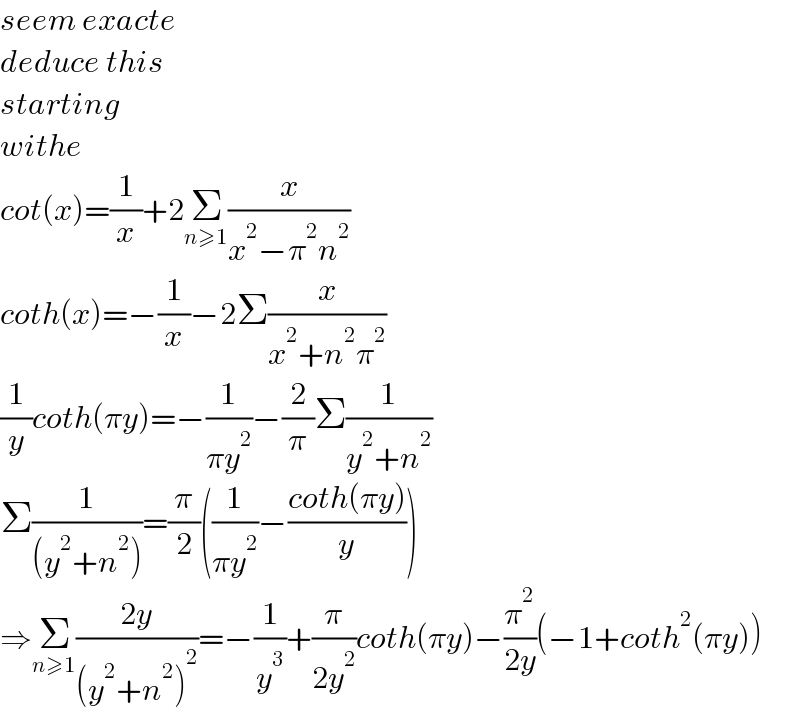
$${seem}\:{exacte}\: \\ $$$${deduce}\:{this} \\ $$$${starting} \\ $$$${withe}\: \\ $$$${cot}\left({x}\right)=\frac{\mathrm{1}}{{x}}+\mathrm{2}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{x}}{{x}^{\mathrm{2}} −\pi^{\mathrm{2}} {n}^{\mathrm{2}} } \\ $$$${coth}\left({x}\right)=−\frac{\mathrm{1}}{{x}}−\mathrm{2}\Sigma\frac{{x}}{{x}^{\mathrm{2}} +{n}^{\mathrm{2}} \pi^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{y}}{coth}\left(\pi{y}\right)=−\frac{\mathrm{1}}{\pi{y}^{\mathrm{2}} }−\frac{\mathrm{2}}{\pi}\Sigma\frac{\mathrm{1}}{{y}^{\mathrm{2}} +{n}^{\mathrm{2}} } \\ $$$$\Sigma\frac{\mathrm{1}}{\left({y}^{\mathrm{2}} +{n}^{\mathrm{2}} \right)}=\frac{\pi}{\mathrm{2}}\left(\frac{\mathrm{1}}{\pi{y}^{\mathrm{2}} }−\frac{{coth}\left(\pi{y}\right)}{{y}}\right) \\ $$$$\Rightarrow\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{2}{y}}{\left({y}^{\mathrm{2}} +{n}^{\mathrm{2}} \right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{{y}^{\mathrm{3}} }+\frac{\pi}{\mathrm{2}{y}^{\mathrm{2}} }{coth}\left(\pi{y}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{2}{y}}\left(−\mathrm{1}+{coth}^{\mathrm{2}} \left(\pi{y}\right)\right) \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com