Question Number 142595 by qaz last updated on 02/Jun/21
![Prove :: sec^2 x=4Σ_(n=0) ^∞ {(1/([(2n+1)π−2x]^2 ))+(1/([(2n+1)π+2x]^2 ))}](https://www.tinkutara.com/question/Q142595.png)
$$\mathrm{Prove}\:::\:\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}=\mathrm{4}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left\{\frac{\mathrm{1}}{\left[\left(\mathrm{2n}+\mathrm{1}\right)\pi−\mathrm{2x}\right]^{\mathrm{2}} }+\frac{\mathrm{1}}{\left[\left(\mathrm{2n}+\mathrm{1}\right)\pi+\mathrm{2x}\right]^{\mathrm{2}} }\right\} \\ $$
Answered by Dwaipayan Shikari last updated on 02/Jun/21
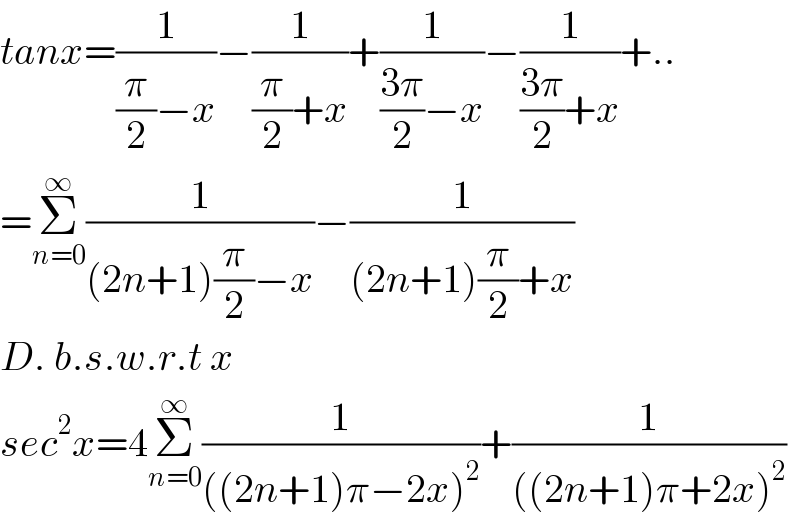
$${tanx}=\frac{\mathrm{1}}{\frac{\pi}{\mathrm{2}}−{x}}−\frac{\mathrm{1}}{\frac{\pi}{\mathrm{2}}+{x}}+\frac{\mathrm{1}}{\frac{\mathrm{3}\pi}{\mathrm{2}}−{x}}−\frac{\mathrm{1}}{\frac{\mathrm{3}\pi}{\mathrm{2}}+{x}}+.. \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}}−{x}}−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}}+{x}} \\ $$$${D}.\:{b}.{s}.{w}.{r}.{t}\:{x} \\ $$$${sec}^{\mathrm{2}} {x}=\mathrm{4}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\left(\mathrm{2}{n}+\mathrm{1}\right)\pi−\mathrm{2}{x}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\left(\mathrm{2}{n}+\mathrm{1}\right)\pi+\mathrm{2}{x}\right)^{\mathrm{2}} } \\ $$
