Question Number 12688 by frank ntulah last updated on 29/Apr/17
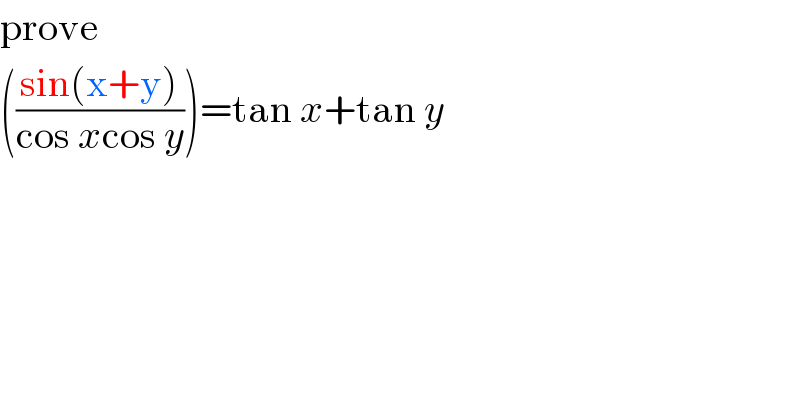
$$\mathrm{prove}\: \\ $$$$\left(\frac{\mathrm{sin}\left(\mathrm{x}+\mathrm{y}\right)}{\mathrm{cos}\:{x}\mathrm{cos}\:{y}}\right)=\mathrm{tan}\:{x}+\mathrm{tan}\:{y} \\ $$
Answered by nume1114 last updated on 29/Apr/17
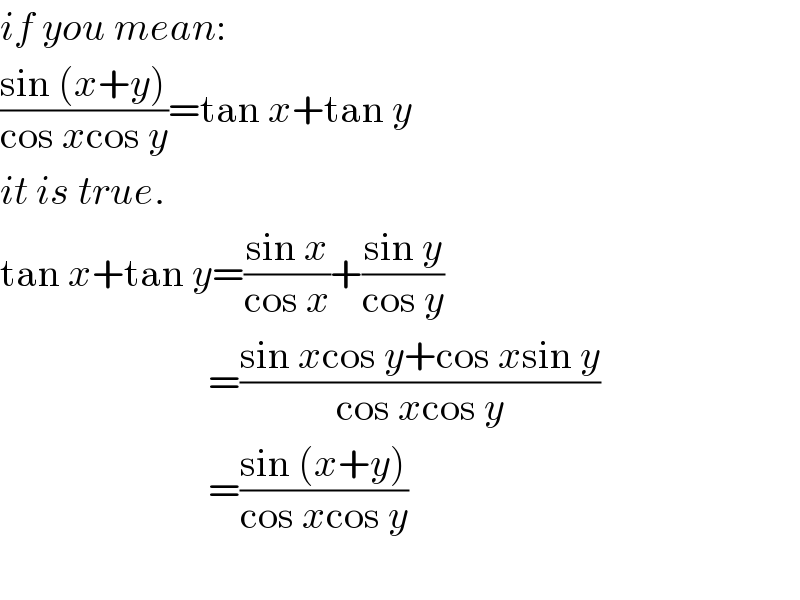
$${if}\:{you}\:{mean}: \\ $$$$\frac{\mathrm{sin}\:\left({x}+{y}\right)}{\mathrm{cos}\:{x}\mathrm{cos}\:{y}}=\mathrm{tan}\:{x}+\mathrm{tan}\:{y}\:\: \\ $$$${it}\:{is}\:{true}. \\ $$$$\mathrm{tan}\:{x}+\mathrm{tan}\:{y}=\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}+\frac{\mathrm{sin}\:{y}}{\mathrm{cos}\:{y}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{sin}\:{x}\mathrm{cos}\:{y}+\mathrm{cos}\:{x}\mathrm{sin}\:{y}}{\mathrm{cos}\:{x}\mathrm{cos}\:{y}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{sin}\:\left({x}+{y}\right)}{\mathrm{cos}\:{x}\mathrm{cos}\:{y}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by frank ntulah last updated on 29/Apr/17
$$\mathrm{you}\:\mathrm{are}\:\mathrm{right}\:\mathrm{sir},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{a}\:\mathrm{lot}\: \\ $$
