Question Number 76680 by Tony Lin last updated on 29/Dec/19
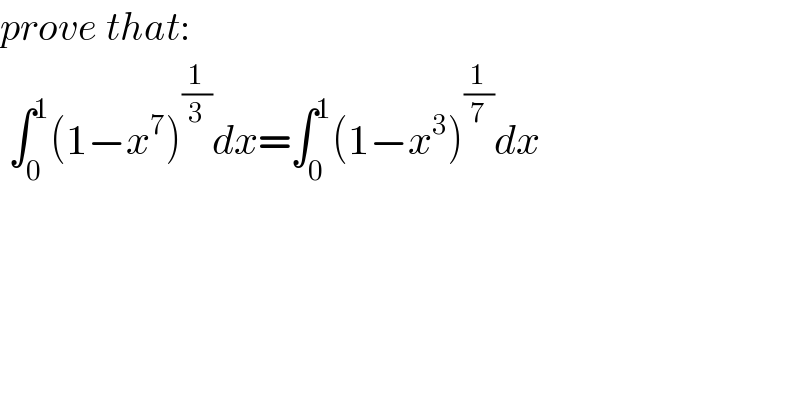
$${prove}\:{that}: \\ $$$$\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{7}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} {dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{7}}} {dx} \\ $$
Commented by mr W last updated on 29/Dec/19

$${see}\:{Q}#\mathrm{76232},\:\mathrm{76146} \\ $$$$\int_{{a}} ^{{b}} {y}\left({x}\right)\:{dx}=\int_{{c}} ^{{d}} {x}\left({y}\right)\:{dy} \\ $$$${y}=\left(\mathrm{1}−{x}^{\mathrm{7}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\Rightarrow{y}^{\mathrm{3}} =\mathrm{1}−{x}^{\mathrm{7}} \\ $$$$\Rightarrow{x}=\left(\mathrm{1}−{y}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{7}}} \\ $$$${y}\left({a}=\mathrm{0}\right)=\mathrm{1}={d} \\ $$$${y}\left({b}=\mathrm{1}\right)=\mathrm{0}={c} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {y}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{7}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left({y}\right){dy}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{y}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{7}}} {dy} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{7}}} {dx} \\ $$
Commented by mr W last updated on 29/Dec/19
$${both}\:{integrals}\:{represent}\:{the}\:{same} \\ $$$${shaded}\:{area}: \\ $$
Commented by mr W last updated on 29/Dec/19

Commented by Tony Lin last updated on 29/Dec/19

$${thanks}\:{sir} \\ $$
