Question Number 139912 by mnjuly1970 last updated on 02/May/21
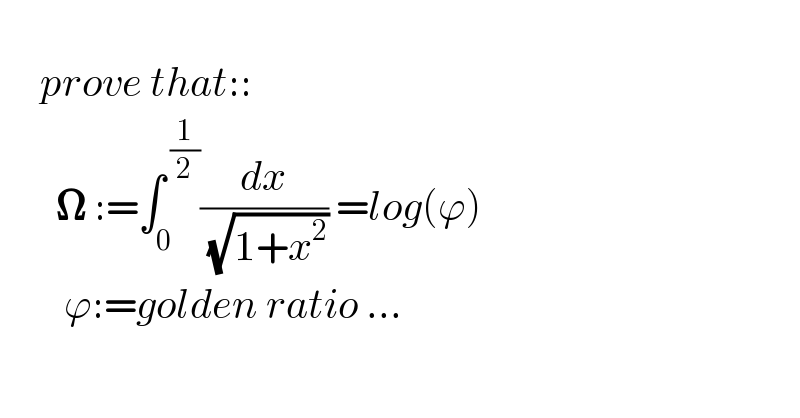
$$ \\ $$$$\:\:\:\:\:{prove}\:{that}::\: \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\Omega}\::=\int_{\mathrm{0}} ^{\:\frac{\mathrm{1}}{\mathrm{2}}} \frac{{dx}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:={log}\left(\varphi\right) \\ $$$$\:\:\:\:\:\:\:\:\varphi:={golden}\:{ratio}\:… \\ $$$$ \\ $$
Answered by qaz last updated on 02/May/21

$$\int_{\mathrm{0}} ^{\mathrm{1}/\mathrm{2}} \frac{{dx}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}={ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\mid_{\mathrm{0}} ^{\mathrm{1}/\mathrm{2}} ={ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$
Commented by mnjuly1970 last updated on 02/May/21

$$\:\:{very}\:{nice}\:… \\ $$
