Menu Close

prove-that-0-101101110-irrational-number-

Tinku Tara 0 Comments
Pin




Question Number 4670 by malwaan last updated on 20/Feb/16
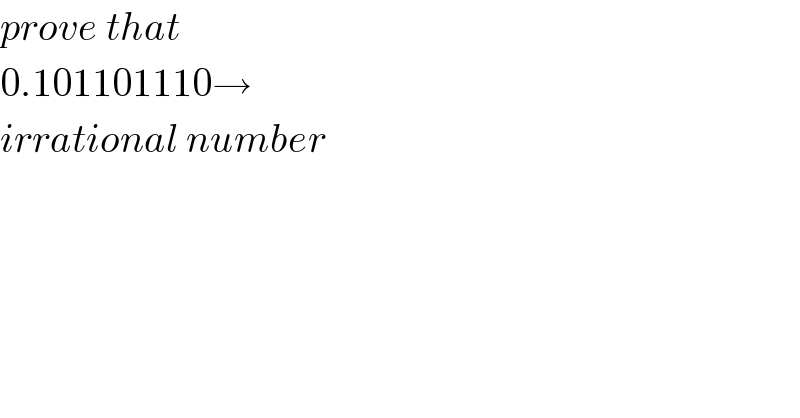
prove that 0.101101110→ irrational number
$${prove}\:{that} \\ $$$$\mathrm{0}.\mathrm{101101110}\rightarrow\: \\ $$$${irrational}\:{number} \\ $$
Commented by prakash jain last updated on 21/Feb/16
Non−recurring non−terminating decimals are irrational.
$$\mathrm{Non}−\mathrm{recurring}\:\mathrm{non}−\mathrm{terminating}\:\mathrm{decimals} \\ $$$$\mathrm{are}\:\mathrm{irrational}. \\ $$
Commented by malwaan last updated on 21/Feb/16
Is there mathematical prove?
$${Is}\:{there}\:{mathematical}\:{prove}? \\ $$
Commented by 123456 last updated on 21/Feb/16
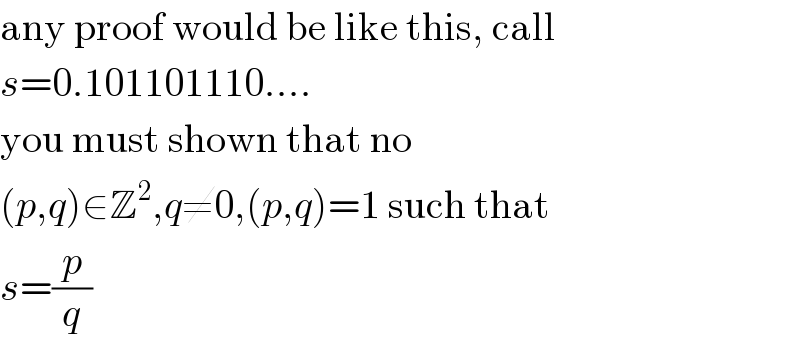
any proof would be like this, call s=0.101101110.... you must shown that no (p,q)∈Z^2 ,q≠0,(p,q)=1 such that s=(p/q)
$$\mathrm{any}\:\mathrm{proof}\:\mathrm{would}\:\mathrm{be}\:\mathrm{like}\:\mathrm{this},\:\mathrm{call} \\ $$$${s}=\mathrm{0}.\mathrm{101101110}…. \\ $$$$\mathrm{you}\:\mathrm{must}\:\mathrm{shown}\:\mathrm{that}\:\mathrm{no} \\ $$$$\left({p},{q}\right)\in\mathbb{Z}^{\mathrm{2}} ,{q}\neq\mathrm{0},\left({p},{q}\right)=\mathrm{1}\:\mathrm{such}\:\mathrm{that} \\ $$$${s}=\frac{{p}}{{q}} \\ $$
Commented by FilupSmith last updated on 22/Feb/16
a_1 =0.1=(1/(10)) a_2 =0.0011=((11)/(10^ )) a_3 =0.00000111=((111)/(10^8 )) a_4 =0.0000000001111=((1111)/(10^(13) )) a_5 =0.0000000000000011111=((11111)/(10^(19) )) a_6 =0.00000000000000000000111111=((111111)/(10^(26) )) ⋮ a_n =(((111...1_(n−ones) ))/(10^k )), k_n =0, 1, 4, 8, 13, 19, 26, ... According to Wolfram Alpha k=−(((n−2)^2 n)/((n−1)^3 )) A=Σ_(i=1) ^∞ a_i A=0.101101110=(1/(10))+((11)/(10^4 ))+((111)/(10^8 ))+... Prove RHS is irrational
$${a}_{\mathrm{1}} =\mathrm{0}.\mathrm{1}=\frac{\mathrm{1}}{\mathrm{10}} \\ $$$${a}_{\mathrm{2}} =\mathrm{0}.\mathrm{0011}=\frac{\mathrm{11}}{\mathrm{10}^{} } \\ $$$${a}_{\mathrm{3}} =\mathrm{0}.\mathrm{00000111}=\frac{\mathrm{111}}{\mathrm{10}^{\mathrm{8}} } \\ $$$${a}_{\mathrm{4}} =\mathrm{0}.\mathrm{0000000001111}=\frac{\mathrm{1111}}{\mathrm{10}^{\mathrm{13}} } \\ $$$${a}_{\mathrm{5}} =\mathrm{0}.\mathrm{0000000000000011111}=\frac{\mathrm{11111}}{\mathrm{10}^{\mathrm{19}} } \\ $$$${a}_{\mathrm{6}} =\mathrm{0}.\mathrm{00000000000000000000111111}=\frac{\mathrm{111111}}{\mathrm{10}^{\mathrm{26}} } \\ $$$$\vdots \\ $$$${a}_{{n}} =\frac{\left(\underset{\mathrm{n}−\mathrm{ones}} {\mathrm{111}…\mathrm{1}}\right)}{\mathrm{10}^{{k}} },\:{k}_{{n}} =\mathrm{0},\:\mathrm{1},\:\mathrm{4},\:\mathrm{8},\:\mathrm{13},\:\mathrm{19},\:\mathrm{26},\:… \\ $$$$\mathrm{According}\:\mathrm{to}\:\mathrm{Wolfram}\:\mathrm{Alpha} \\ $$$${k}=−\frac{\left({n}−\mathrm{2}\right)^{\mathrm{2}} {n}}{\left({n}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${A}=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{a}_{{i}} \\ $$$${A}=\mathrm{0}.\mathrm{101101110}=\frac{\mathrm{1}}{\mathrm{10}}+\frac{\mathrm{11}}{\mathrm{10}^{\mathrm{4}} }+\frac{\mathrm{111}}{\mathrm{10}^{\mathrm{8}} }+… \\ $$$$\mathrm{Prove}\:\mathrm{RHS}\:\mathrm{is}\:\mathrm{irrational} \\ $$
Commented by prakash jain last updated on 22/Feb/16
A number of (p/q) (p,q) is either a teminating decimal or repeatitive decimal. This can be proved easily. So by contradiction the number in example cannot be written in form (p/q).
$$\mathrm{A}\:\mathrm{number}\:\mathrm{of}\:\frac{{p}}{{q}}\:\left({p},{q}\right)\:\mathrm{is}\:\mathrm{either}\:\mathrm{a}\:\mathrm{teminating} \\ $$$$\mathrm{decimal}\:\mathrm{or}\:\mathrm{repeatitive}\:\mathrm{decimal}. \\ $$$$\mathrm{This}\:\mathrm{can}\:\mathrm{be}\:\mathrm{proved}\:\mathrm{easily}. \\ $$$$\mathrm{So}\:\mathrm{by}\:\mathrm{contradiction}\:\mathrm{the}\:\mathrm{number}\:\mathrm{in}\:\mathrm{example} \\ $$$$\mathrm{cannot}\:\mathrm{be}\:\mathrm{written}\:\mathrm{in}\:\mathrm{form}\:\frac{{p}}{{q}}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *