Question Number 140310 by liberty last updated on 06/May/21
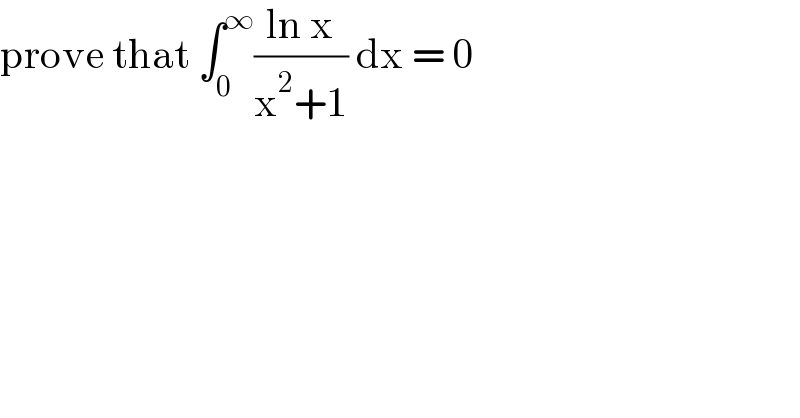
$$\mathrm{prove}\:\mathrm{that}\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{dx}\:=\:\mathrm{0} \\ $$
Answered by qaz last updated on 06/May/21
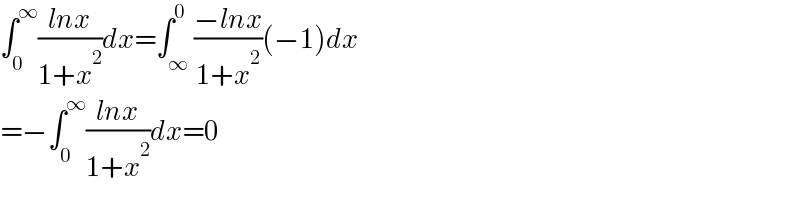
$$\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\int_{\infty} ^{\mathrm{0}} \frac{−{lnx}}{\mathrm{1}+{x}^{\mathrm{2}} }\left(−\mathrm{1}\right){dx} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\mathrm{0} \\ $$
Commented by TheSupreme last updated on 06/May/21
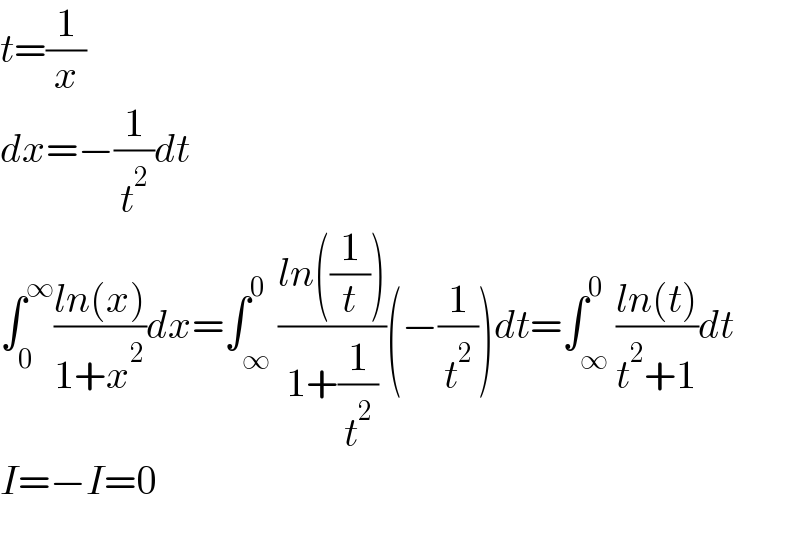
$${t}=\frac{\mathrm{1}}{{x}} \\ $$$${dx}=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }{dt} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\int_{\infty} ^{\mathrm{0}} \frac{{ln}\left(\frac{\mathrm{1}}{{t}}\right)}{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}\left(−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right){dt}=\int_{\infty} ^{\mathrm{0}} \frac{{ln}\left({t}\right)}{{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$${I}=−{I}=\mathrm{0} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 06/May/21
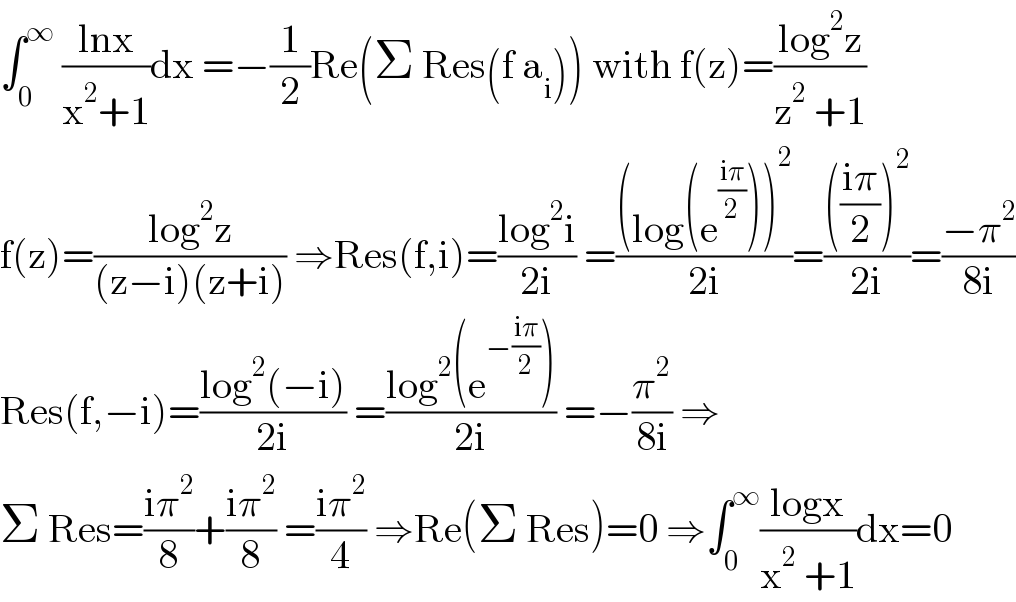
$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\Sigma\:\mathrm{Res}\left(\mathrm{f}\:\mathrm{a}_{\mathrm{i}} \right)\right)\:\mathrm{with}\:\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{log}^{\mathrm{2}} \mathrm{z}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{log}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}−\mathrm{i}\right)\left(\mathrm{z}+\mathrm{i}\right)}\:\Rightarrow\mathrm{Res}\left(\mathrm{f},\mathrm{i}\right)=\frac{\mathrm{log}^{\mathrm{2}} \mathrm{i}}{\mathrm{2i}}\:=\frac{\left(\mathrm{log}\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2}}} \right)\right)^{\mathrm{2}} }{\mathrm{2i}}=\frac{\left(\frac{\mathrm{i}\pi}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2i}}=\frac{−\pi^{\mathrm{2}} }{\mathrm{8i}} \\ $$$$\mathrm{Res}\left(\mathrm{f},−\mathrm{i}\right)=\frac{\mathrm{log}^{\mathrm{2}} \left(−\mathrm{i}\right)}{\mathrm{2i}}\:=\frac{\mathrm{log}^{\mathrm{2}} \left(\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{2}}} \right)}{\mathrm{2i}}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{8i}}\:\Rightarrow \\ $$$$\Sigma\:\mathrm{Res}=\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{8}}+\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{8}}\:=\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{4}}\:\Rightarrow\mathrm{Re}\left(\Sigma\:\mathrm{Res}\right)=\mathrm{0}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{logx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}=\mathrm{0} \\ $$
