Question Number 12826 by malwaan last updated on 03/May/17
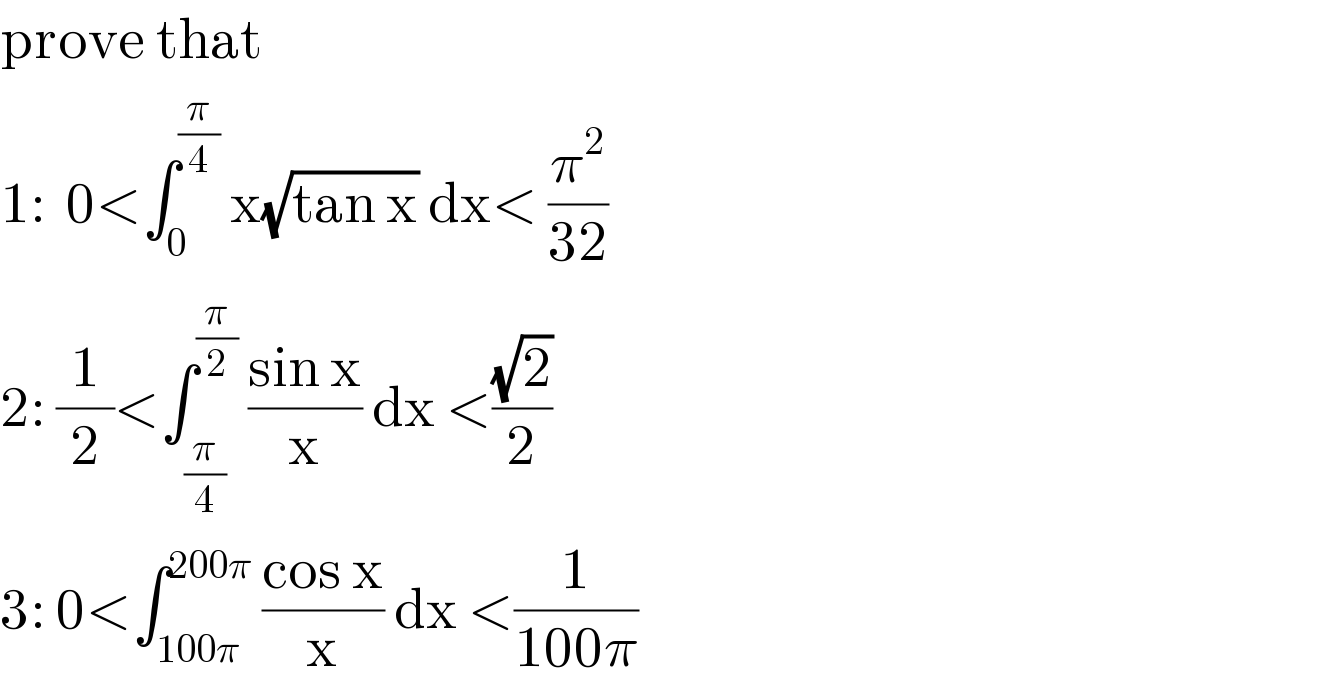
$$\mathrm{prove}\:\mathrm{that} \\ $$$$\mathrm{1}:\:\:\mathrm{0}<\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{x}\sqrt{\mathrm{tan}\:\mathrm{x}}\:\mathrm{dx}<\:\frac{\pi^{\mathrm{2}} }{\mathrm{32}} \\ $$$$\mathrm{2}:\:\frac{\mathrm{1}}{\mathrm{2}}<\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\:\mathrm{dx}\:<\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\mathrm{3}:\:\mathrm{0}<\int_{\mathrm{100}\pi} ^{\mathrm{200}\pi} \:\frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{x}}\:\mathrm{dx}\:<\frac{\mathrm{1}}{\mathrm{100}\pi} \\ $$
