Question Number 142646 by naka3546 last updated on 03/Jun/21
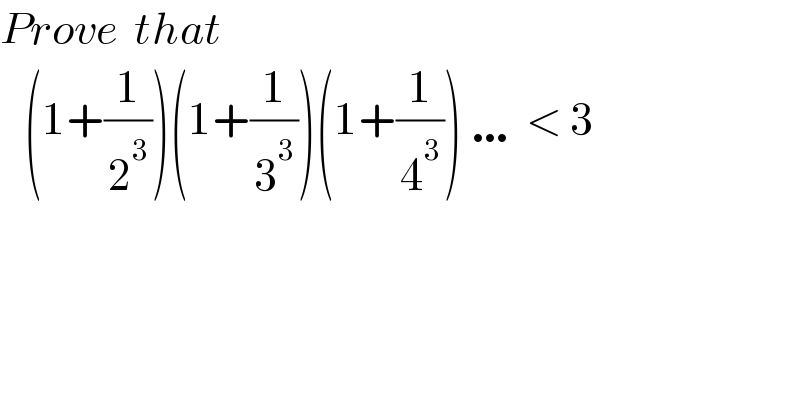
$${Prove}\:\:{that} \\ $$$$\:\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{3}} }\right)\:\ldots\:<\:\mathrm{3} \\ $$
Answered by 1549442205PVT last updated on 04/Jun/21
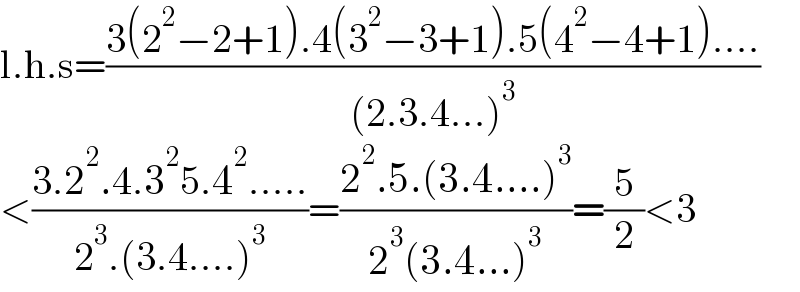
$$\mathrm{l}.\mathrm{h}.\mathrm{s}=\frac{\mathrm{3}\left(\mathrm{2}^{\mathrm{2}} −\mathrm{2}+\mathrm{1}\right).\mathrm{4}\left(\mathrm{3}^{\mathrm{2}} −\mathrm{3}+\mathrm{1}\right).\mathrm{5}\left(\mathrm{4}^{\mathrm{2}} −\mathrm{4}+\mathrm{1}\right)….}{\left(\mathrm{2}.\mathrm{3}.\mathrm{4}…\right)^{\mathrm{3}} } \\ $$$$<\frac{\mathrm{3}.\mathrm{2}^{\mathrm{2}} .\mathrm{4}.\mathrm{3}^{\mathrm{2}} \mathrm{5}.\mathrm{4}^{\mathrm{2}} …..}{\mathrm{2}^{\mathrm{3}} .\left(\mathrm{3}.\mathrm{4}….\right)^{\mathrm{3}} }=\frac{\mathrm{2}^{\mathrm{2}} .\mathrm{5}.\left(\mathrm{3}.\mathrm{4}….\right)^{\mathrm{3}} }{\mathrm{2}^{\mathrm{3}} \left(\mathrm{3}.\mathrm{4}…\right)^{\mathrm{3}} }=\frac{\mathrm{5}}{\mathrm{2}}<\mathrm{3} \\ $$
Commented by naka3546 last updated on 04/Jun/21
$$\mathrm{Dank}\:\mathrm{you}\:,,,\:\mathrm{thank}\:\mathrm{you} \\ $$
