Question Number 73560 by mhmd last updated on 13/Nov/19
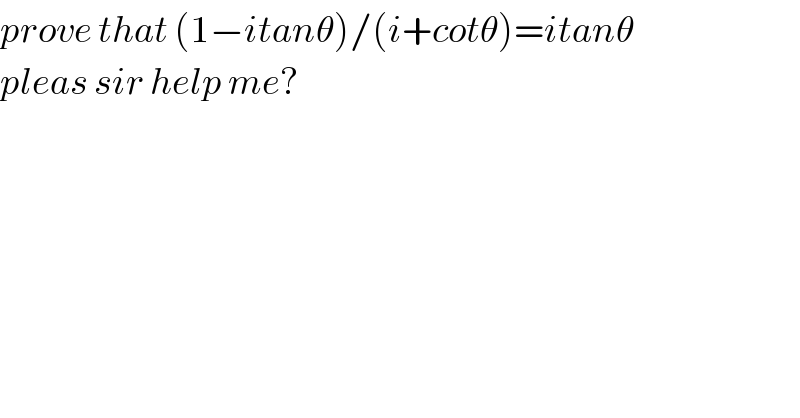
$${prove}\:{that}\:\left(\mathrm{1}−{itan}\theta\right)/\left({i}+{cot}\theta\right)={itan}\theta \\ $$$${pleas}\:{sir}\:{help}\:{me}? \\ $$
Commented by MJS last updated on 13/Nov/19
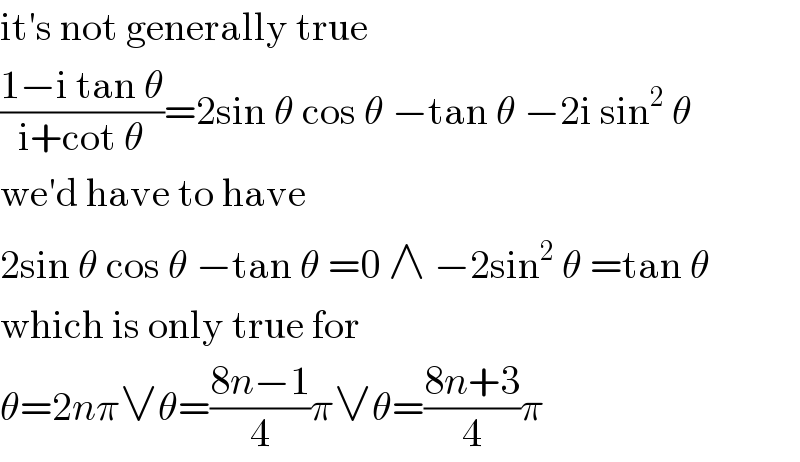
$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{generally}\:\mathrm{true} \\ $$$$\frac{\mathrm{1}−\mathrm{i}\:\mathrm{tan}\:\theta}{\mathrm{i}+\mathrm{cot}\:\theta}=\mathrm{2sin}\:\theta\:\mathrm{cos}\:\theta\:−\mathrm{tan}\:\theta\:−\mathrm{2i}\:\mathrm{sin}^{\mathrm{2}} \:\theta \\ $$$$\mathrm{we}'\mathrm{d}\:\mathrm{have}\:\mathrm{to}\:\mathrm{have} \\ $$$$\mathrm{2sin}\:\theta\:\mathrm{cos}\:\theta\:−\mathrm{tan}\:\theta\:=\mathrm{0}\:\wedge\:−\mathrm{2sin}^{\mathrm{2}} \:\theta\:=\mathrm{tan}\:\theta \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{only}\:\mathrm{true}\:\mathrm{for} \\ $$$$\theta=\mathrm{2}{n}\pi\vee\theta=\frac{\mathrm{8}{n}−\mathrm{1}}{\mathrm{4}}\pi\vee\theta=\frac{\mathrm{8}{n}+\mathrm{3}}{\mathrm{4}}\pi \\ $$
Answered by ajfour last updated on 13/Nov/19

$$\frac{\mathrm{1}−{i}\mathrm{tan}\:\theta}{{i}+\mathrm{cot}\:\theta}=\frac{\left(\mathrm{1}−{i}\mathrm{tan}\:\theta\right)\left(\mathrm{tan}\:\theta\right)}{\mathrm{1}+{i}\mathrm{tan}\:\theta} \\ $$$$=\left(\mathrm{1}−{i}\mathrm{tan}\:\theta\right)^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$$={e}^{−\mathrm{2}{i}\theta} \mathrm{tan}\:\theta \\ $$$$.. \\ $$
