Question Number 10539 by malwaan last updated on 17/Feb/17
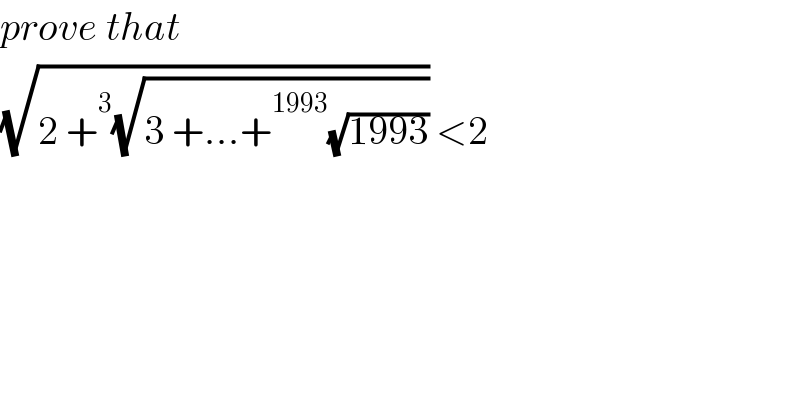
$${prove}\:{that} \\ $$$$\sqrt{\mathrm{2}\:+\overset{\mathrm{3}} {\:}\sqrt{\mathrm{3}\:+…+\overset{\mathrm{1993}} {\:}\sqrt{\mathrm{1993}}}}\:<\mathrm{2} \\ $$
Answered by mrW1 last updated on 17/Feb/17

$${function}\:{y}=\left({x}+{a}\right)^{\frac{\mathrm{1}}{{x}}} \:{with}\:{a}>\mathrm{1}\:{is} \\ $$$${for}\:{x}>\mathrm{0}\:{strictly}\:{decreasing},\:{that} \\ $$$${means} \\ $$$$\:^{\mathrm{3}} \sqrt{\mathrm{3}+{a}}<\sqrt{\mathrm{2}+{a}} \\ $$$$\:^{\mathrm{4}} \sqrt{\mathrm{4}+{a}}<\sqrt{\mathrm{2}+{a}} \\ $$$$…… \\ $$$$\:^{\mathrm{1993}} \sqrt{\mathrm{1993}+{a}}<\sqrt{\mathrm{2}+{a}} \\ $$$$…… \\ $$$$\:^{{n}} \sqrt{{n}+{a}}<\sqrt{\mathrm{2}+{a}} \\ $$$$…… \\ $$$$ \\ $$$${A}=\sqrt{\mathrm{2}\:+\overset{\mathrm{3}} {\:}\sqrt{\mathrm{3}\:+…+\overset{\mathrm{1993}} {\:}\sqrt{\mathrm{1993}}}}\:\:\:\left({finite}\right) \\ $$$$<\sqrt{\mathrm{2}\:+\overset{\mathrm{3}} {\:}\sqrt{\mathrm{3}\:+…+\overset{\mathrm{1993}} {\:}\sqrt{\mathrm{1993}+\:^{\mathrm{1994}} \sqrt{\mathrm{1994}+….}}}}\:\:\:\left({infinite}\right) \\ $$$$<\sqrt{\mathrm{2}\:+\:\sqrt{\mathrm{2}\:+…+\:\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+…}}}}\:={x} \\ $$$$ \\ $$$$\sqrt{\mathrm{2}\:+\:\sqrt{\mathrm{2}\:+…+\:\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+…}}}}\:={x} \\ $$$$\mathrm{2}+{x}={x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{2}=\mathrm{0} \\ $$$$\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${since}\:{x}>\mathrm{0}, \\ $$$$\Rightarrow{x}=\mathrm{2} \\ $$$$\therefore\:{A}=\sqrt{\mathrm{2}\:+\overset{\mathrm{3}} {\:}\sqrt{\mathrm{3}\:+…+\overset{\mathrm{1993}} {\:}\sqrt{\mathrm{1993}}}}<{x}=\mathrm{2} \\ $$
Commented by FilupS last updated on 18/Feb/17
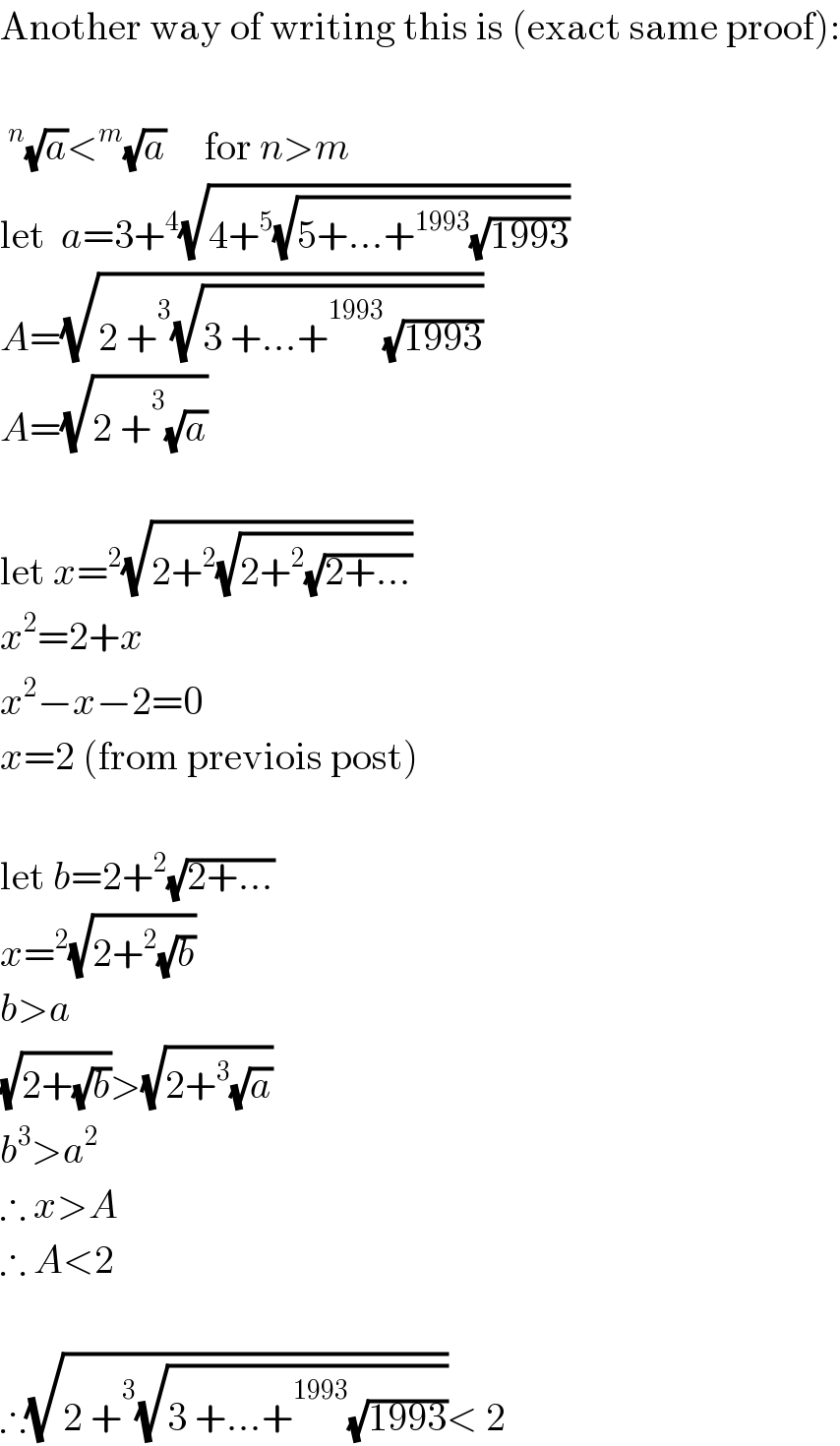
$$\mathrm{Another}\:\mathrm{way}\:\mathrm{of}\:\mathrm{writing}\:\mathrm{this}\:\mathrm{is}\:\left(\mathrm{exact}\:\mathrm{same}\:\mathrm{proof}\right): \\ $$$$\: \\ $$$$\:^{{n}} \sqrt{{a}}<^{{m}} \sqrt{{a}}\:\:\:\:\:\mathrm{for}\:{n}>{m} \\ $$$$\mathrm{let}\:\:{a}=\mathrm{3}+^{\mathrm{4}} \sqrt{\mathrm{4}+^{\mathrm{5}} \sqrt{\mathrm{5}+…+^{\mathrm{1993}} \sqrt{\mathrm{1993}}}} \\ $$$${A}=\sqrt{\mathrm{2}\:+\overset{\mathrm{3}} {\:}\sqrt{\mathrm{3}\:+…+\overset{\mathrm{1993}} {\:}\sqrt{\mathrm{1993}}}} \\ $$$${A}=\sqrt{\mathrm{2}\:+\overset{\mathrm{3}} {\:}\sqrt{{a}}} \\ $$$$\: \\ $$$$\mathrm{let}\:{x}=^{\mathrm{2}} \sqrt{\mathrm{2}+^{\mathrm{2}} \sqrt{\mathrm{2}+^{\mathrm{2}} \sqrt{\mathrm{2}+…}}} \\ $$$${x}^{\mathrm{2}} =\mathrm{2}+{x} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{2}=\mathrm{0} \\ $$$${x}=\mathrm{2}\:\left(\mathrm{from}\:\mathrm{previois}\:\mathrm{post}\right) \\ $$$$\: \\ $$$$\mathrm{let}\:{b}=\mathrm{2}+^{\mathrm{2}} \sqrt{\mathrm{2}+…} \\ $$$${x}=^{\mathrm{2}} \sqrt{\mathrm{2}+^{\mathrm{2}} \sqrt{{b}}} \\ $$$${b}>{a} \\ $$$$\sqrt{\mathrm{2}+\sqrt{{b}}}>\sqrt{\mathrm{2}+^{\mathrm{3}} \sqrt{{a}}} \\ $$$${b}^{\mathrm{3}} >{a}^{\mathrm{2}} \\ $$$$\therefore\:{x}>{A} \\ $$$$\therefore\:{A}<\mathrm{2} \\ $$$$\: \\ $$$$\therefore\sqrt{\mathrm{2}\:+\overset{\mathrm{3}} {\:}\sqrt{\mathrm{3}\:+…+\overset{\mathrm{1993}} {\:}\sqrt{\mathrm{1993}}}}<\:\mathrm{2} \\ $$
Commented by malwaan last updated on 20/Feb/17
$${thank}\:{you}\:{so}\:{much} \\ $$
