Prove-that-2-4-G-Potential-of-Gravitational-field-Density-G-Universal-Gravitational-Constant-

Question Number 137970 by Dwaipayan Shikari last updated on 08/Apr/21

Prove that ▽^2 𝛗=−4𝛑Gρ φ=Potential of Gravitational field ρ=Density G=Universal Gravitational Constant

$${Prove}\:{that}\: \\ $$$$\bigtriangledown^{\mathrm{2}} \boldsymbol{\phi}=−\mathrm{4}\boldsymbol{\pi{G}}\rho\:\: \\ $$$$\phi={Potential}\:{of}\:{Gravitational}\:{field} \\ $$$$\rho={Density}\:\:\:\boldsymbol{{G}}={Universal}\:{Gravitational}\:{Constant} \\ $$

Answered by ajfour last updated on 08/Apr/21

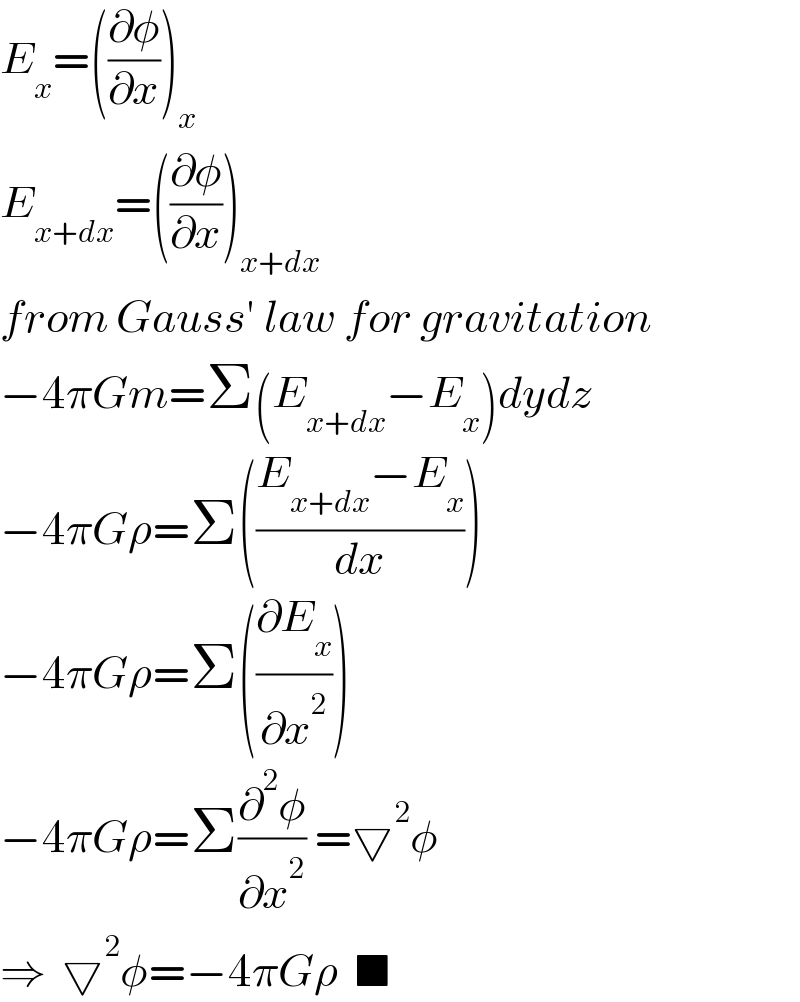
E_x =((∂φ/∂x))_x E_(x+dx) =((∂φ/∂x))_(x+dx) from Gauss′ law for gravitation −4πGm=Σ(E_(x+dx) −E_x )dydz −4πGρ=Σ(((E_(x+dx) −E_x )/dx)) −4πGρ=Σ((∂E_x /∂x^2 )) −4πGρ=Σ(∂^2 φ/∂x^2 ) =▽^2 φ ⇒ ▽^2 φ=−4πGρ ■

$${E}_{{x}} =\left(\frac{\partial\phi}{\partial{x}}\right)_{{x}} \\ $$$${E}_{{x}+{dx}} =\left(\frac{\partial\phi}{\partial{x}}\right)_{{x}+{dx}} \\ $$$${from}\:{Gauss}'\:{law}\:{for}\:{gravitation} \\ $$$$−\mathrm{4}\pi{Gm}=\Sigma\left({E}_{{x}+{dx}} −{E}_{{x}} \right){dydz} \\ $$$$−\mathrm{4}\pi{G}\rho=\Sigma\left(\frac{{E}_{{x}+{dx}} −{E}_{{x}} }{{dx}}\right) \\ $$$$−\mathrm{4}\pi{G}\rho=\Sigma\left(\frac{\partial{E}_{{x}} }{\partial{x}^{\mathrm{2}} }\right) \\ $$$$−\mathrm{4}\pi{G}\rho=\Sigma\frac{\partial^{\mathrm{2}} \phi}{\partial{x}^{\mathrm{2}} }\:=\bigtriangledown^{\mathrm{2}} \phi \\ $$$$\Rightarrow\:\:\bigtriangledown^{\mathrm{2}} \phi=−\mathrm{4}\pi{G}\rho\:\:\blacksquare \\ $$

Commented by Dwaipayan Shikari last updated on 08/Apr/21

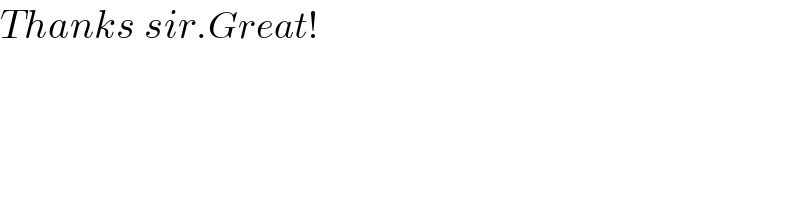
$${Thanks}\:{sir}.{Great}! \\ $$

Commented by Dwaipayan Shikari last updated on 08/Apr/21

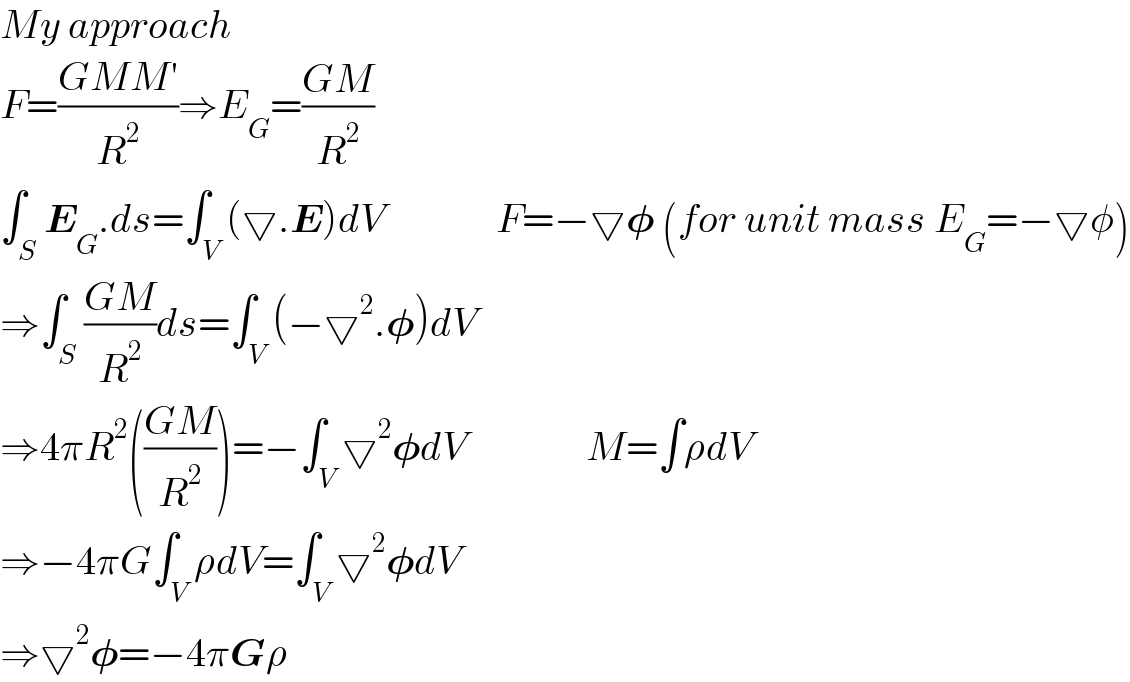
My approach F=((GMM′)/R^2 )⇒E_G =((GM)/R^2 ) ∫_S E_G .ds=∫_V (▽.E)dV F=−▽𝛗 (for unit mass E_G =−▽φ) ⇒∫_S ((GM)/R^2 )ds=∫_V (−▽^2 .𝛗)dV ⇒4πR^2 (((GM)/R^2 ))=−∫_V ▽^2 𝛗dV M=∫ρdV ⇒−4πG∫_V ρdV=∫_V ▽^2 𝛗dV ⇒▽^2 𝛗=−4πGρ

$${My}\:{approach} \\ $$$${F}=\frac{{GMM}'}{{R}^{\mathrm{2}} }\Rightarrow{E}_{{G}} =\frac{{GM}}{{R}^{\mathrm{2}} } \\ $$$$\int_{{S}} \boldsymbol{{E}}_{{G}} .{ds}=\int_{{V}} \left(\bigtriangledown.\boldsymbol{{E}}\right){dV}\:\:\:\:\:\:\:\:\:\:\:\:\:\:{F}=−\bigtriangledown\boldsymbol{\phi}\:\left({for}\:{unit}\:{mass}\:{E}_{{G}} =−\bigtriangledown\phi\right) \\ $$$$\Rightarrow\int_{{S}} \frac{{GM}}{{R}^{\mathrm{2}} }{ds}=\int_{{V}} \left(−\bigtriangledown^{\mathrm{2}} .\boldsymbol{\phi}\right){dV} \\ $$$$\Rightarrow\mathrm{4}\pi{R}^{\mathrm{2}} \left(\frac{{GM}}{{R}^{\mathrm{2}} }\right)=−\int_{{V}} \bigtriangledown^{\mathrm{2}} \boldsymbol{\phi}{dV}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{M}=\int\rho{dV} \\ $$$$\Rightarrow−\mathrm{4}\pi{G}\int_{{V}} \rho{dV}=\int_{{V}} \bigtriangledown^{\mathrm{2}} \boldsymbol{\phi}{dV} \\ $$$$\Rightarrow\bigtriangledown^{\mathrm{2}} \boldsymbol{\phi}=−\mathrm{4}\pi\boldsymbol{{G}}\rho \\ $$

Facebook Tweet Pin

Prove-that-2-4-G-Potential-of-Gravitational-field-Density-G-Universal-Gravitational-Constant-

Leave a Reply Cancel reply