Question Number 2777 by Filup last updated on 27/Nov/15
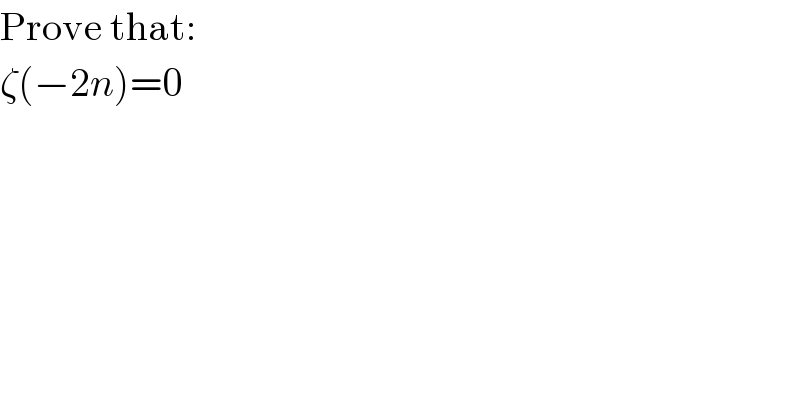
$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\zeta\left(−\mathrm{2}{n}\right)=\mathrm{0} \\ $$
Answered by prakash jain last updated on 27/Nov/15
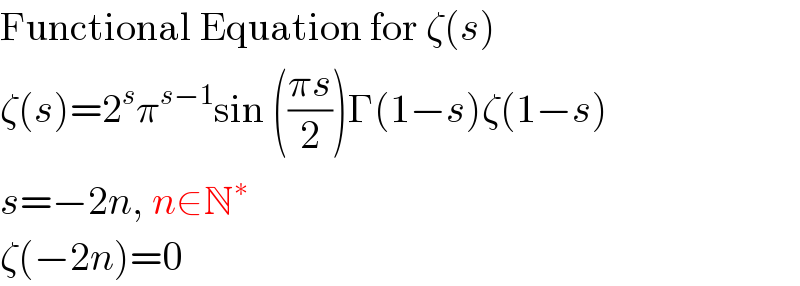
$$\mathrm{Functional}\:\mathrm{Equation}\:\mathrm{for}\:\zeta\left({s}\right) \\ $$$$\zeta\left({s}\right)=\mathrm{2}^{{s}} \pi^{{s}−\mathrm{1}} \mathrm{sin}\:\left(\frac{\pi{s}}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}−{s}\right)\zeta\left(\mathrm{1}−{s}\right) \\ $$$${s}=−\mathrm{2}{n},\:{n}\in\mathbb{N}^{\ast} \\ $$$$\zeta\left(−\mathrm{2}{n}\right)=\mathrm{0} \\ $$
Commented by 123456 last updated on 27/Nov/15

$${n}\in\mathbb{N}^{\ast} \\ $$
Commented by prakash jain last updated on 27/Nov/15

$$\mathrm{corrected}. \\ $$
