Menu Close

prove-that-5555-2222-2222-5555-is-divisible-by-7-

Tinku Tara 0 Comments
Pin




Question Number 772 by malwaan last updated on 12/Mar/15
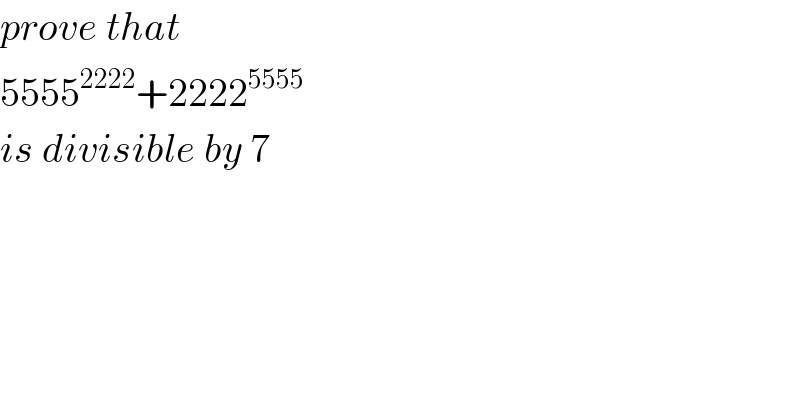
prove that 5555^(2222) +2222^(5555) is divisible by 7
$${prove}\:{that}\: \\ $$$$\mathrm{5555}^{\mathrm{2222}} +\mathrm{2222}^{\mathrm{5555}} \: \\ $$$${is}\:{divisible}\:{by}\:\mathrm{7} \\ $$
Commented by 123456 last updated on 10/Mar/15
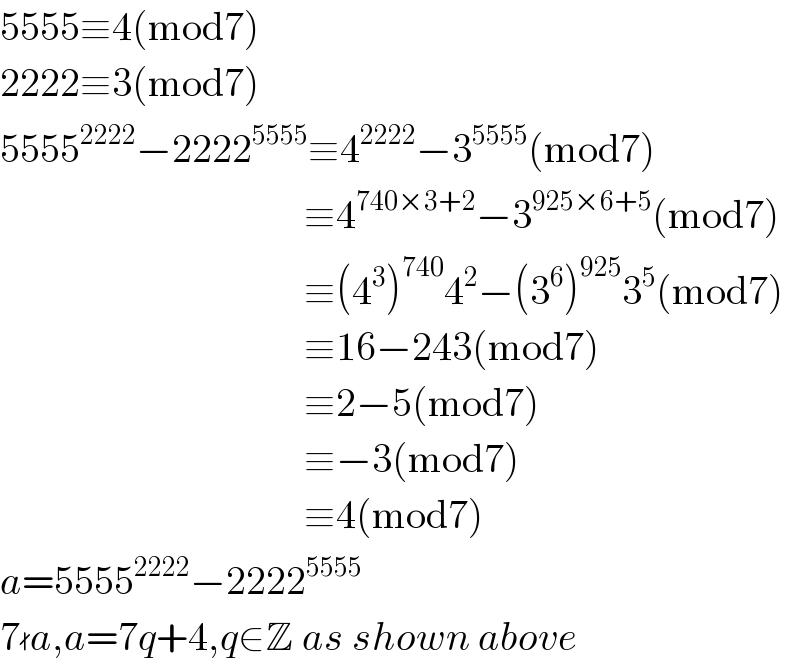
5555≡4(mod7) 2222≡3(mod7) 5555^(2222) −2222^(5555) ≡4^(2222) −3^(5555) (mod7) ≡4^(740×3+2) −3^(925×6+5) (mod7) ≡(4^3 )^(740) 4^2 −(3^6 )^(925) 3^5 (mod7) ≡16−243(mod7) ≡2−5(mod7) ≡−3(mod7) ≡4(mod7) a=5555^(2222) −2222^(5555) 7a,a=7q+4,q∈Z as shown above
$$\mathrm{5555}\equiv\mathrm{4}\left(\mathrm{mod7}\right) \\ $$$$\mathrm{2222}\equiv\mathrm{3}\left(\mathrm{mod7}\right) \\ $$$$\mathrm{5555}^{\mathrm{2222}} −\mathrm{2222}^{\mathrm{5555}} \equiv\mathrm{4}^{\mathrm{2222}} −\mathrm{3}^{\mathrm{5555}} \left(\mathrm{mod7}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\equiv\mathrm{4}^{\mathrm{740}×\mathrm{3}+\mathrm{2}} −\mathrm{3}^{\mathrm{925}×\mathrm{6}+\mathrm{5}} \left(\mathrm{mod7}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\equiv\left(\mathrm{4}^{\mathrm{3}} \right)^{\mathrm{740}} \mathrm{4}^{\mathrm{2}} −\left(\mathrm{3}^{\mathrm{6}} \right)^{\mathrm{925}} \mathrm{3}^{\mathrm{5}} \left(\mathrm{mod7}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\equiv\mathrm{16}−\mathrm{243}\left(\mathrm{mod7}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\equiv\mathrm{2}−\mathrm{5}\left(\mathrm{mod7}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\equiv−\mathrm{3}\left(\mathrm{mod7}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\equiv\mathrm{4}\left(\mathrm{mod7}\right) \\ $$$${a}=\mathrm{5555}^{\mathrm{2222}} −\mathrm{2222}^{\mathrm{5555}} \\ $$$$\mathrm{7}\nshortmid{a},{a}=\mathrm{7}{q}+\mathrm{4},{q}\in\mathbb{Z}\:{as}\:{shown}\:{above} \\ $$
Commented by prakash jain last updated on 10/Mar/15
5555^(2222) −2222^(5555) is not divisible by7. 5555^(2222) +2222^(5555) is divisible by 7.
$$\mathrm{5555}^{\mathrm{2222}} −\mathrm{2222}^{\mathrm{5555}} \:\mathrm{is}\:\mathrm{not}\:\mathrm{divisible}\:\mathrm{by7}. \\ $$$$\mathrm{5555}^{\mathrm{2222}} +\mathrm{2222}^{\mathrm{5555}} \:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{7}. \\ $$
Commented by malwaan last updated on 12/Mar/15
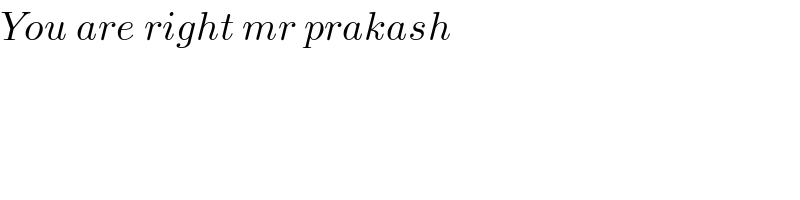
You are right mr prakash
$${You}\:{are}\:{right}\:{mr}\:{prakash} \\ $$
Commented by prakash jain last updated on 12/Mar/15
The answer given in earlier comment by 123456 proves your updated question. 5555^(2222) +2222^(5555) ≡0 (mod 7)
$$\mathrm{The}\:\mathrm{answer}\:\mathrm{given}\:\mathrm{in}\:\mathrm{earlier}\:\mathrm{comment}\:\mathrm{by} \\ $$$$\mathrm{123456}\:\mathrm{proves}\:\mathrm{your}\:\mathrm{updated}\:\mathrm{question}. \\ $$$$\mathrm{5555}^{\mathrm{2222}} +\mathrm{2222}^{\mathrm{5555}} \equiv\mathrm{0}\:\left(\mathrm{mod}\:\mathrm{7}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *