Question Number 72145 by Maclaurin Stickker last updated on 25/Oct/19
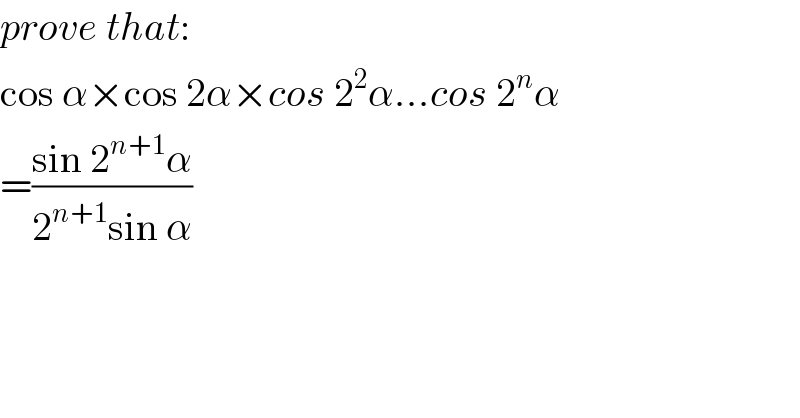
$${prove}\:{that}: \\ $$$$\mathrm{cos}\:\alpha×\mathrm{cos}\:\mathrm{2}\alpha×{cos}\:\mathrm{2}^{\mathrm{2}} \alpha…{cos}\:\mathrm{2}^{{n}} \alpha \\ $$$$=\frac{\mathrm{sin}\:\mathrm{2}^{{n}+\mathrm{1}} \alpha}{\mathrm{2}^{{n}+\mathrm{1}} \mathrm{sin}\:\alpha} \\ $$$$ \\ $$
Commented by kaivan.ahmadi last updated on 25/Oct/19

$${first}\:{way}\::{we}\:{solve}\:{by}\:{induction} \\ $$$${n}=\mathrm{1}\Rightarrow\frac{{sin}\mathrm{2}^{\mathrm{2}} \alpha}{\mathrm{2}^{\mathrm{2}} {sin}\alpha}=\frac{{sin}\mathrm{2}\alpha{cos}\mathrm{2}\alpha}{\mathrm{2}{sin}\alpha}={cos}\alpha{cos}\mathrm{2}\alpha \\ $$$${induction}\:{hypothesis} \\ $$$${n}={k}−\mathrm{1}\Rightarrow{cos}\alpha×{cos}\mathrm{2}\alpha×…×{cos}\mathrm{2}^{{k}−\mathrm{1}} \alpha=\frac{{sin}\mathrm{2}^{{k}} \alpha}{\mathrm{2}^{{k}} {sin}\alpha} \\ $$$${now} \\ $$$${n}={k}\Rightarrow{cos}\alpha×{cos}\mathrm{2}\alpha×…×{cos}\mathrm{2}^{{k}−\mathrm{1}} \alpha×{cos}\mathrm{2}^{{k}} \alpha= \\ $$$$\frac{{sin}\mathrm{2}^{{k}} \alpha{cos}\mathrm{2}^{{k}} \alpha}{\mathrm{2}^{{k}} {sin}\alpha}=\frac{\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}^{{k}+\mathrm{1}} \alpha}{\mathrm{2}^{{k}} {sin}\alpha}=\frac{{sin}\mathrm{2}^{{k}+\mathrm{1}} \alpha}{\mathrm{2}^{{k}+\mathrm{1}} {sin}\alpha}. \\ $$$$ \\ $$$$ \\ $$$${second}\:{way}: \\ $$$$ \\ $$$$\frac{{sin}\mathrm{2}^{{n}+\mathrm{1}} \alpha}{\mathrm{2}^{{n}+\mathrm{1}} {sin}\alpha}=\frac{{sin}\mathrm{2}^{{n}} \alpha{cos}\mathrm{2}^{{n}} \alpha}{\mathrm{2}^{{n}} {sin}\alpha}=\frac{{sin}\mathrm{2}^{{n}−\mathrm{1}} \alpha{cos}\mathrm{2}^{{n}−\mathrm{1}} \alpha{cos}\mathrm{2}^{{n}} \alpha}{\mathrm{2}^{{n}−\mathrm{1}} {sin}\alpha}= \\ $$$$…=\frac{{sin}\mathrm{2}^{\mathrm{0}} \alpha{cos}\mathrm{2}^{\mathrm{0}} \alpha{cos}\mathrm{2}\alpha…{cos}\mathrm{2}^{{n}} \alpha}{{sin}\alpha}= \\ $$$${cos}\alpha{cos}\mathrm{2}\alpha…{cos}\mathrm{2}^{{n}} \alpha \\ $$$$ \\ $$
Commented by Maclaurin Stickker last updated on 25/Oct/19
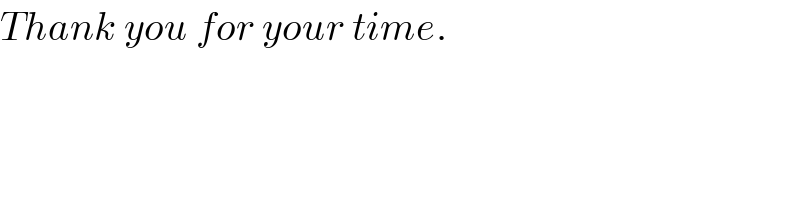
$${Thank}\:{you}\:{for}\:{your}\:{time}. \\ $$
Commented by mathmax by abdo last updated on 25/Oct/19
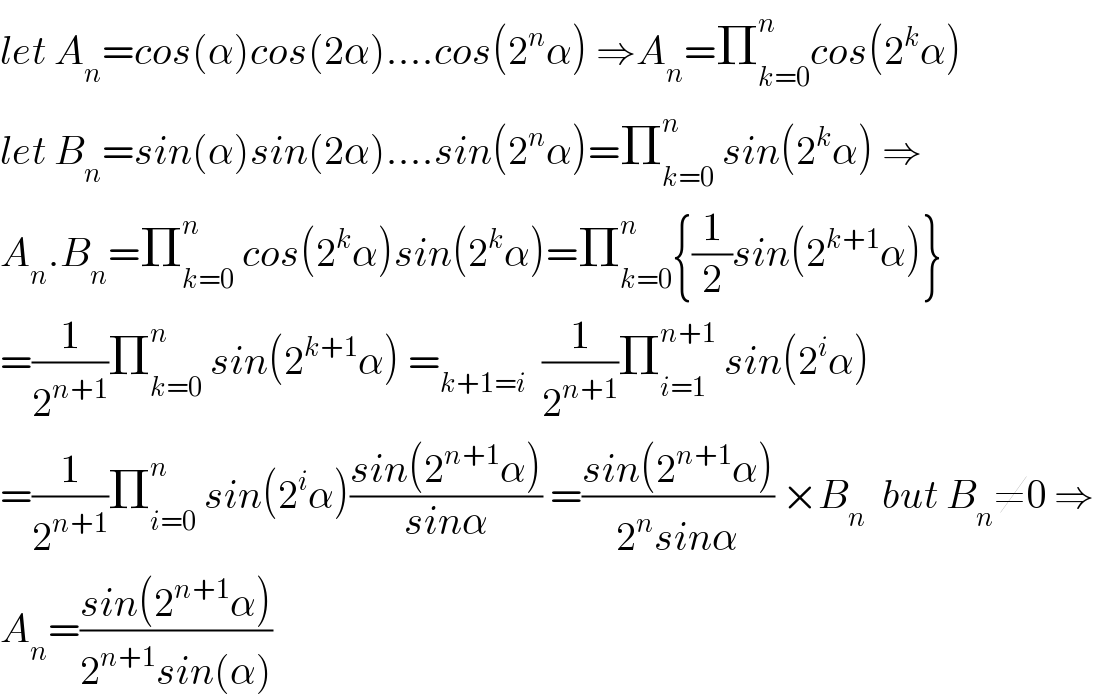
$${let}\:{A}_{{n}} ={cos}\left(\alpha\right){cos}\left(\mathrm{2}\alpha\right)….{cos}\left(\mathrm{2}^{{n}} \alpha\right)\:\Rightarrow{A}_{{n}} =\prod_{{k}=\mathrm{0}} ^{{n}} {cos}\left(\mathrm{2}^{{k}} \alpha\right) \\ $$$${let}\:{B}_{{n}} ={sin}\left(\alpha\right){sin}\left(\mathrm{2}\alpha\right)….{sin}\left(\mathrm{2}^{{n}} \alpha\right)=\prod_{{k}=\mathrm{0}} ^{{n}} \:{sin}\left(\mathrm{2}^{{k}} \alpha\right)\:\Rightarrow \\ $$$${A}_{{n}} .{B}_{{n}} =\prod_{{k}=\mathrm{0}} ^{{n}} \:{cos}\left(\mathrm{2}^{{k}} \alpha\right){sin}\left(\mathrm{2}^{{k}} \alpha\right)=\prod_{{k}=\mathrm{0}} ^{{n}} \left\{\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}^{{k}+\mathrm{1}} \alpha\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }\prod_{{k}=\mathrm{0}} ^{{n}} \:{sin}\left(\mathrm{2}^{{k}+\mathrm{1}} \alpha\right)\:=_{{k}+\mathrm{1}={i}} \:\:\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }\prod_{{i}=\mathrm{1}} ^{{n}+\mathrm{1}} \:{sin}\left(\mathrm{2}^{{i}} \alpha\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }\prod_{{i}=\mathrm{0}} ^{{n}} \:{sin}\left(\mathrm{2}^{{i}} \alpha\right)\frac{{sin}\left(\mathrm{2}^{{n}+\mathrm{1}} \alpha\right)}{{sin}\alpha}\:=\frac{{sin}\left(\mathrm{2}^{{n}+\mathrm{1}} \alpha\right)}{\mathrm{2}^{{n}} {sin}\alpha}\:×{B}_{{n}} \:\:{but}\:{B}_{{n}} \neq\mathrm{0}\:\Rightarrow \\ $$$${A}_{{n}} =\frac{{sin}\left(\mathrm{2}^{{n}+\mathrm{1}} \alpha\right)}{\mathrm{2}^{{n}+\mathrm{1}} {sin}\left(\alpha\right)} \\ $$
Commented by mathmax by abdo last updated on 25/Oct/19
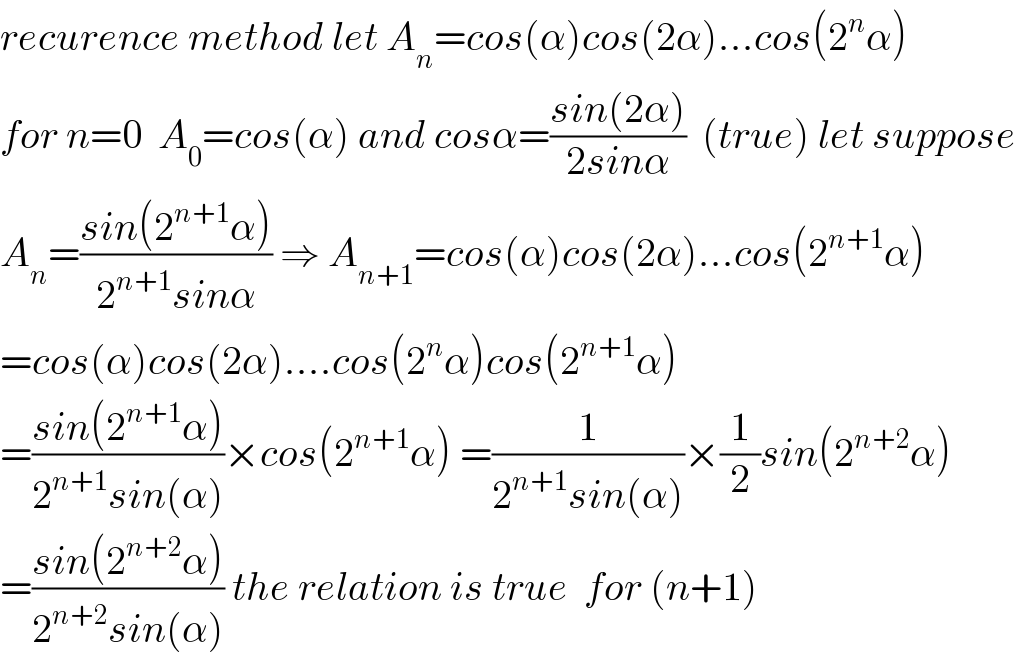
$${recurence}\:{method}\:{let}\:{A}_{{n}} ={cos}\left(\alpha\right){cos}\left(\mathrm{2}\alpha\right)…{cos}\left(\mathrm{2}^{{n}} \alpha\right) \\ $$$${for}\:{n}=\mathrm{0}\:\:{A}_{\mathrm{0}} ={cos}\left(\alpha\right)\:{and}\:{cos}\alpha=\frac{{sin}\left(\mathrm{2}\alpha\right)}{\mathrm{2}{sin}\alpha}\:\:\left({true}\right)\:{let}\:{suppose} \\ $$$${A}_{{n}} =\frac{{sin}\left(\mathrm{2}^{{n}+\mathrm{1}} \alpha\right)}{\mathrm{2}^{{n}+\mathrm{1}} {sin}\alpha}\:\Rightarrow\:{A}_{{n}+\mathrm{1}} ={cos}\left(\alpha\right){cos}\left(\mathrm{2}\alpha\right)…{cos}\left(\mathrm{2}^{{n}+\mathrm{1}} \alpha\right) \\ $$$$={cos}\left(\alpha\right){cos}\left(\mathrm{2}\alpha\right)….{cos}\left(\mathrm{2}^{{n}} \alpha\right){cos}\left(\mathrm{2}^{{n}+\mathrm{1}} \alpha\right) \\ $$$$=\frac{{sin}\left(\mathrm{2}^{{n}+\mathrm{1}} \alpha\right)}{\mathrm{2}^{{n}+\mathrm{1}} {sin}\left(\alpha\right)}×{cos}\left(\mathrm{2}^{{n}+\mathrm{1}} \alpha\right)\:=\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} {sin}\left(\alpha\right)}×\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}^{{n}+\mathrm{2}} \alpha\right) \\ $$$$=\frac{{sin}\left(\mathrm{2}^{{n}+\mathrm{2}} \alpha\right)}{\mathrm{2}^{{n}+\mathrm{2}} {sin}\left(\alpha\right)}\:{the}\:{relation}\:{is}\:{true}\:\:{for}\:\left({n}+\mathrm{1}\right) \\ $$
