Question Number 73243 by mathmax by abdo last updated on 09/Nov/19
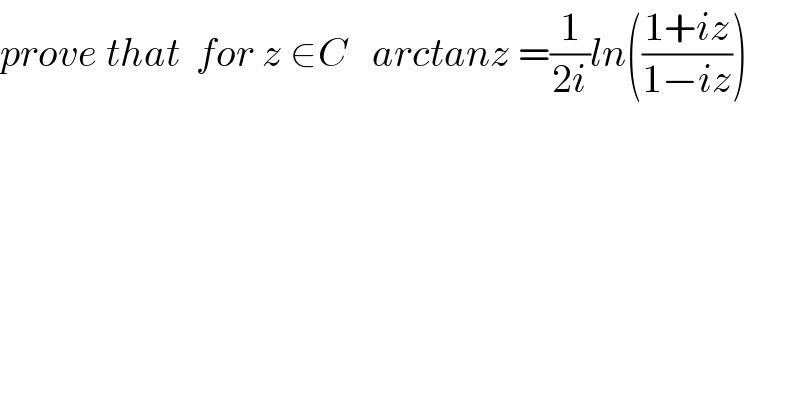
$${prove}\:{that}\:\:{for}\:{z}\:\in{C}\:\:\:{arctanz}\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}+{iz}}{\mathrm{1}−{iz}}\right) \\ $$$$ \\ $$
Answered by mr W last updated on 09/Nov/19
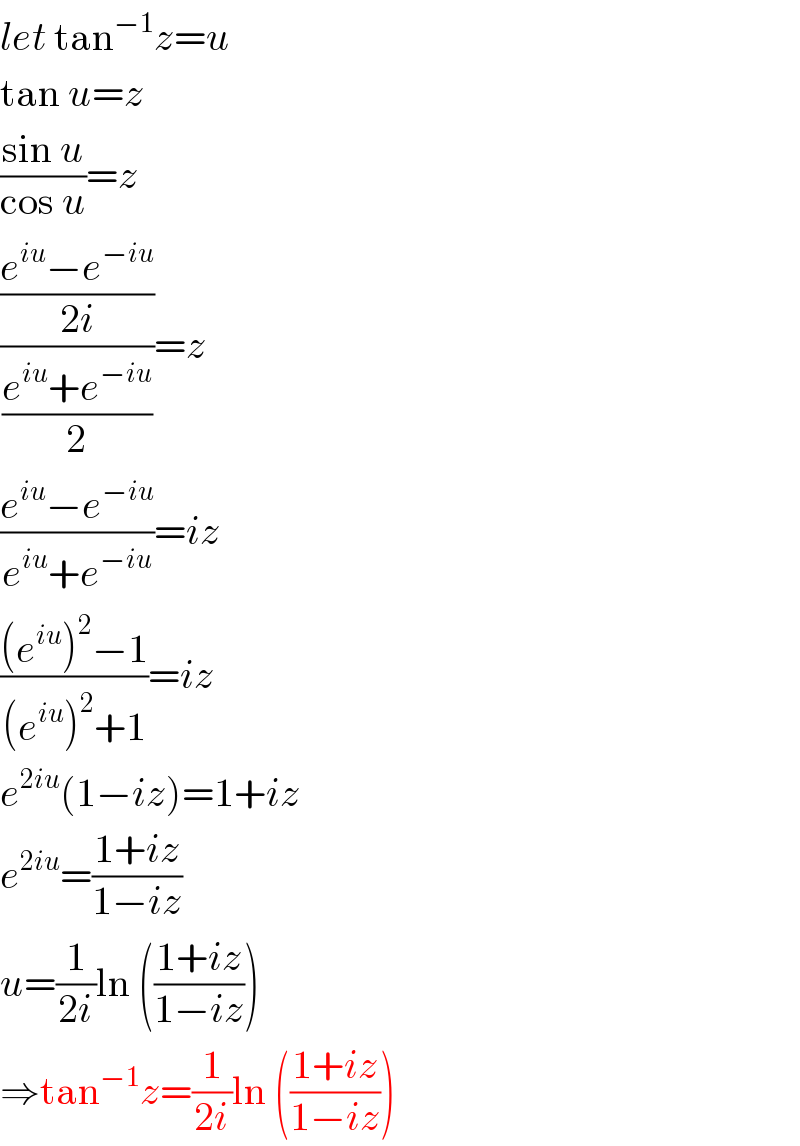
$${let}\:\mathrm{tan}^{−\mathrm{1}} {z}={u} \\ $$$$\mathrm{tan}\:{u}={z} \\ $$$$\frac{\mathrm{sin}\:{u}}{\mathrm{cos}\:{u}}={z} \\ $$$$\frac{\frac{{e}^{{iu}} −{e}^{−{iu}} }{\mathrm{2}{i}}}{\frac{{e}^{{iu}} +{e}^{−{iu}} }{\mathrm{2}}}={z} \\ $$$$\frac{{e}^{{iu}} −{e}^{−{iu}} }{{e}^{{iu}} +{e}^{−{iu}} }={iz} \\ $$$$\frac{\left({e}^{{iu}} \right)^{\mathrm{2}} −\mathrm{1}}{\left({e}^{{iu}} \right)^{\mathrm{2}} +\mathrm{1}}={iz} \\ $$$${e}^{\mathrm{2}{iu}} \left(\mathrm{1}−{iz}\right)=\mathrm{1}+{iz} \\ $$$${e}^{\mathrm{2}{iu}} =\frac{\mathrm{1}+{iz}}{\mathrm{1}−{iz}} \\ $$$${u}=\frac{\mathrm{1}}{\mathrm{2}{i}}\mathrm{ln}\:\left(\frac{\mathrm{1}+{iz}}{\mathrm{1}−{iz}}\right) \\ $$$$\Rightarrow\mathrm{tan}^{−\mathrm{1}} {z}=\frac{\mathrm{1}}{\mathrm{2}{i}}\mathrm{ln}\:\left(\frac{\mathrm{1}+{iz}}{\mathrm{1}−{iz}}\right) \\ $$
Commented by mathmax by abdo last updated on 09/Nov/19

$${thankx}\:{sir}\:{mrw}. \\ $$
