prove-that-H-n-k-1-n-1-k-1-k-C-n-k-H-n-k-1-n-1-k-

Question Number 73043 by mathmax by abdo last updated on 05/Nov/19

prove that H_n =Σ_(k=1) ^n (((−1)^(k+1) )/k)×C_n ^k H_n =Σ_(k=1) ^n (1/k)

$${prove}\:{that}\:{H}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{{k}}×{C}_{{n}} ^{{k}} \\ $$$${H}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}} \\ $$

Commented by mind is power last updated on 06/Nov/19

B(1,n)=(1/n) mad this in my anwer .i put (1/(n+1)) but i took (1/n) i csn′t change is pictur that i saved

$$\mathrm{B}\left(\mathrm{1},\mathrm{n}\right)=\frac{\mathrm{1}}{\mathrm{n}}\:\mathrm{mad}\:\mathrm{this}\:\mathrm{in}\:\mathrm{my}\:\mathrm{anwer}\:.\mathrm{i}\:\mathrm{put}\:\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\:\mathrm{but}\:\mathrm{i}\:\mathrm{took}\:\frac{\mathrm{1}}{\mathrm{n}} \\ $$$$\mathrm{i}\:\mathrm{csn}'\mathrm{t}\:\mathrm{change}\:\mathrm{is}\:\mathrm{pictur}\:\mathrm{that}\:\mathrm{i}\:\mathrm{saved} \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 06/Nov/19

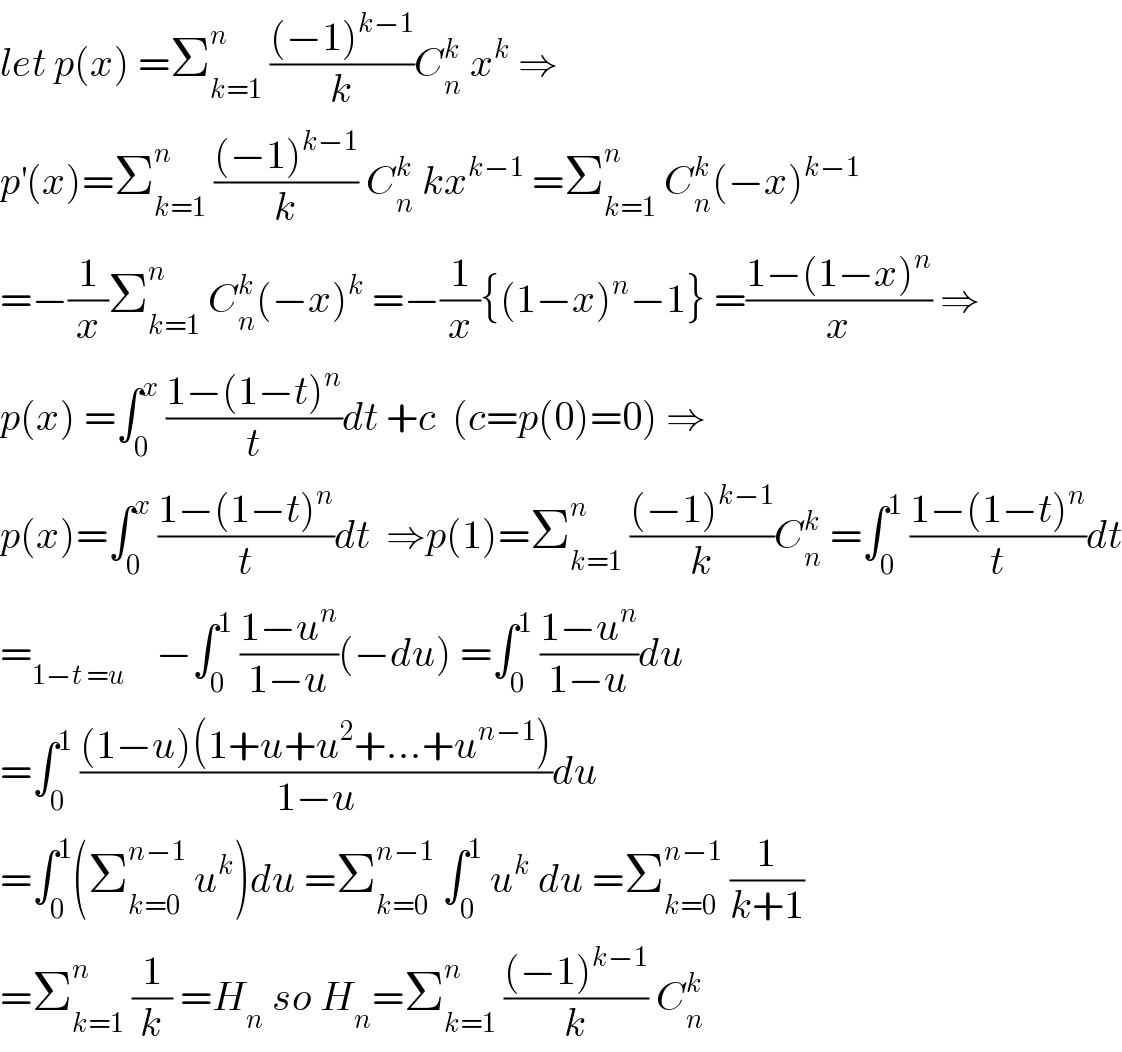
let p(x) =Σ_(k=1) ^n (((−1)^(k−1) )/k)C_n ^k x^k ⇒ p^′ (x)=Σ_(k=1) ^n (((−1)^(k−1) )/k) C_n ^k kx^(k−1) =Σ_(k=1) ^n C_n ^k (−x)^(k−1) =−(1/x)Σ_(k=1) ^n C_n ^k (−x)^k =−(1/x){(1−x)^n −1} =((1−(1−x)^n )/x) ⇒ p(x) =∫_0 ^x ((1−(1−t)^n )/t)dt +c (c=p(0)=0) ⇒ p(x)=∫_0 ^x ((1−(1−t)^n )/t)dt ⇒p(1)=Σ_(k=1) ^n (((−1)^(k−1) )/k)C_n ^k =∫_0 ^1 ((1−(1−t)^n )/t)dt =_(1−t =u) −∫_0 ^1 ((1−u^n )/(1−u))(−du) =∫_0 ^1 ((1−u^n )/(1−u))du =∫_0 ^1 (((1−u)(1+u+u^2 +...+u^(n−1) ))/(1−u))du =∫_0 ^1 (Σ_(k=0) ^(n−1) u^k )du =Σ_(k=0) ^(n−1) ∫_0 ^1 u^k du =Σ_(k=0) ^(n−1) (1/(k+1)) =Σ_(k=1) ^n (1/k) =H_n so H_n =Σ_(k=1) ^n (((−1)^(k−1) )/k) C_n ^k

$${let}\:{p}\left({x}\right)\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{{k}}{C}_{{n}} ^{{k}} \:{x}^{{k}} \:\Rightarrow \\ $$$${p}^{'} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{{k}}\:{C}_{{n}} ^{{k}} \:{kx}^{{k}−\mathrm{1}} \:=\sum_{{k}=\mathrm{1}} ^{{n}} \:{C}_{{n}} ^{{k}} \left(−{x}\right)^{{k}−\mathrm{1}} \\ $$$$=−\frac{\mathrm{1}}{{x}}\sum_{{k}=\mathrm{1}} ^{{n}} \:{C}_{{n}} ^{{k}} \left(−{x}\right)^{{k}} \:=−\frac{\mathrm{1}}{{x}}\left\{\left(\mathrm{1}−{x}\right)^{{n}} −\mathrm{1}\right\}\:=\frac{\mathrm{1}−\left(\mathrm{1}−{x}\right)^{{n}} }{{x}}\:\Rightarrow \\ $$$${p}\left({x}\right)\:=\int_{\mathrm{0}} ^{{x}} \:\frac{\mathrm{1}−\left(\mathrm{1}−{t}\right)^{{n}} }{{t}}{dt}\:+{c}\:\:\left({c}={p}\left(\mathrm{0}\right)=\mathrm{0}\right)\:\Rightarrow \\ $$$${p}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \:\frac{\mathrm{1}−\left(\mathrm{1}−{t}\right)^{{n}} }{{t}}{dt}\:\:\Rightarrow{p}\left(\mathrm{1}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{{k}}{C}_{{n}} ^{{k}} \:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−\left(\mathrm{1}−{t}\right)^{{n}} }{{t}}{dt} \\ $$$$=_{\mathrm{1}−{t}\:={u}} \:\:\:\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−{u}^{{n}} }{\mathrm{1}−{u}}\left(−{du}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−{u}^{{n}} }{\mathrm{1}−{u}}{du} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\mathrm{1}−{u}\right)\left(\mathrm{1}+{u}+{u}^{\mathrm{2}} +…+{u}^{{n}−\mathrm{1}} \right)}{\mathrm{1}−{u}}{du} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{u}^{{k}} \right){du}\:=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:{u}^{{k}} \:{du}\:=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{\mathrm{1}}{{k}+\mathrm{1}} \\ $$$$=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:={H}_{{n}} \:{so}\:{H}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{{k}}\:{C}_{{n}} ^{{k}} \\ $$

Answered by mind is power last updated on 06/Nov/19