Question Number 7861 by Yozzia last updated on 21/Sep/16
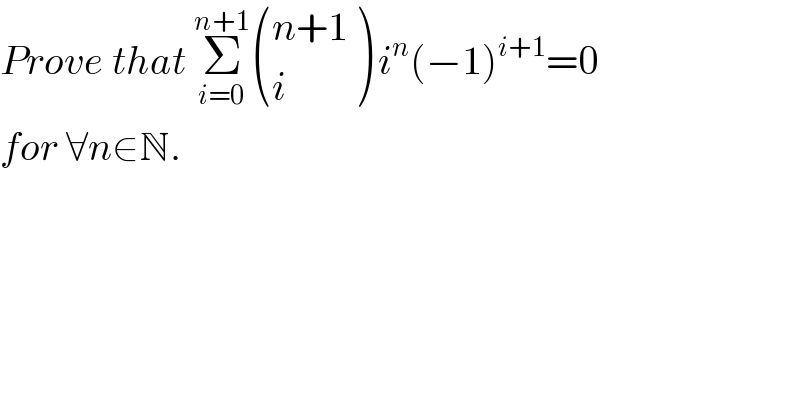
$${Prove}\:{that}\:\underset{{i}=\mathrm{0}} {\overset{{n}+\mathrm{1}} {\sum}}\begin{pmatrix}{{n}+\mathrm{1}}\\{{i}}\end{pmatrix}\:{i}^{{n}} \left(−\mathrm{1}\right)^{{i}+\mathrm{1}} =\mathrm{0}\: \\ $$$${for}\:\forall{n}\in\mathbb{N}. \\ $$
Commented by FilupSmith last updated on 22/Sep/16

$${attempt} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}+\mathrm{1}} {\sum}}\begin{pmatrix}{{n}+\mathrm{1}}\\{{i}}\end{pmatrix}\:=\underset{{i}=\mathrm{0}} {\overset{{k}} {\sum}}\:\frac{{k}!}{{i}!\centerdot\left({k}−{i}\right)!}={k}!\underset{{i}=\mathrm{0}} {\overset{{k}} {\sum}}\:\frac{\mathrm{1}}{{i}!\centerdot\left({k}−{i}\right)!} \\ $$$${n}+\mathrm{1}={k}\:\:\:\Rightarrow\:\:{n}={k}−\mathrm{1} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{k}} {\sum}}{S}={k}!\left(\frac{\mathrm{1}}{\mathrm{0}!×{k}!}+\frac{\mathrm{1}}{\mathrm{1}!×\left({k}−\mathrm{1}\right)!}+\frac{\mathrm{1}}{\mathrm{2}!×\left({k}−\mathrm{2}\right)!}+…+\frac{\mathrm{1}}{\left({k}−\mathrm{1}\right)!×\mathrm{1}!}+\frac{\mathrm{1}}{{k}!×\mathrm{0}!}\right) \\ $$$$\: \\ $$$$\therefore\underset{{i}=\mathrm{0}} {\overset{{n}+\mathrm{1}} {\sum}}\begin{pmatrix}{{n}+\mathrm{1}}\\{{i}}\end{pmatrix}\:{i}^{{n}} \left(−\mathrm{1}\right)^{{n}+\mathrm{1}} =\underset{{i}=\mathrm{0}} {\overset{{k}} {\sum}}{Si}^{{k}−\mathrm{1}} \left(−\mathrm{1}\right)^{{k}} \\ $$$$\: \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{k}} {\sum}}{Si}^{{k}−\mathrm{1}} ={k}!\left(\frac{\mathrm{0}^{{k}−\mathrm{1}} }{\mathrm{0}!×{k}!}+\frac{\mathrm{1}^{{k}−\mathrm{1}} }{\mathrm{1}!×\left({k}−\mathrm{1}\right)!}+\frac{\mathrm{2}^{{k}−\mathrm{1}} }{\mathrm{2}!×\left({k}−\mathrm{2}\right)!}+…+\frac{\left({k}−\mathrm{1}\right)^{{k}−\mathrm{1}} }{\left({k}−\mathrm{1}\right)!×\mathrm{1}!}+\frac{{k}^{{k}−\mathrm{1}} }{{k}!×\mathrm{0}!}\right) \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{k}} {\sum}}{Si}^{{k}−\mathrm{1}} =\frac{\mathrm{0}^{{k}−\mathrm{1}} }{\mathrm{0}!}+\frac{{k}×\mathrm{1}^{{k}−\mathrm{1}} }{\mathrm{1}!}+\frac{{k}\left({k}−\mathrm{1}\right)\mathrm{2}^{{k}−\mathrm{1}} }{\mathrm{2}!}+\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)\mathrm{3}^{{k}−\mathrm{1}} }{\mathrm{3}!}+…+\frac{{k}\left({k}−\mathrm{1}\right)^{{k}−\mathrm{1}} }{\mathrm{1}!}+\frac{{k}^{{k}−\mathrm{1}} }{\mathrm{0}!} \\ $$$$\: \\ $$$$\therefore\underset{{i}=\mathrm{0}} {\overset{{k}} {\sum}}{Si}^{{k}−\mathrm{1}} \left(−\mathrm{1}\right)^{{k}} =\frac{\mathrm{0}^{{k}−\mathrm{1}} }{\mathrm{0}!}+\frac{{k}×\mathrm{1}^{{k}−\mathrm{1}} }{\mathrm{1}!}−\frac{{k}\left({k}−\mathrm{1}\right)\mathrm{2}^{{k}−\mathrm{1}} }{\mathrm{2}!}+\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)\mathrm{3}^{{k}−\mathrm{1}} }{\mathrm{3}!}−…+\frac{{k}\left({k}−\mathrm{1}\right)^{{k}−\mathrm{1}} }{\mathrm{1}!}−\frac{{k}^{{k}−\mathrm{1}} }{\mathrm{0}!} \\ $$$$\mathrm{note}:\:\:\:+\:\mathrm{if}\:\mathrm{previous}\:\mathrm{denominator}\:\mathrm{has}\:\mathrm{a}\:\mathrm{even}\:\mathrm{term} \\ $$$$\therefore\:=\:\frac{\mathrm{0}^{{k}−\mathrm{1}} }{\mathrm{0}!}+\left(\frac{{k}×\mathrm{1}^{{k}−\mathrm{1}} }{\mathrm{1}!}+\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)\mathrm{3}^{{k}−\mathrm{1}} }{\mathrm{3}!}+…\right)−\left(\frac{{k}\left({k}−\mathrm{1}\right)\mathrm{2}^{{k}−\mathrm{1}} }{\mathrm{2}!}+\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)\left({k}−\mathrm{3}\right)\mathrm{4}^{{k}−\mathrm{1}} }{\mathrm{4}!}+…\right) \\ $$$${working} \\ $$$${currently}\:{unsure}\:{how}\:{to}\:{continue} \\ $$
Commented by prakash jain last updated on 01/Oct/16
![f(x)=(1−e^x )^(n+1) =−Σ_(i=0) ^(n+1) ^(n+1) C_i e^(ix) (−1)^(i+1) f^n (x)=−Σ_(i=0) ^n ^(n+1) C_i i^n e^(ix) (−1)^(i+1) =required expression at x=0 Also f(x)=(1−e^x )^(n+1) =LHS f ′(x)=−(n+1)(1−e^x )^n (−e^x ) f^2 (x)=−[(n+1)(e^x )(1−e^x )^n −(n+1)ne^x (1−e^x )^(n−1) (−e^x )] ⋮ f^n (0)=0 [∵(1−e^x ) is factor till n^(th) differentiation] hence −Σ_(i=0) ^n ^(n+1) C_i i^n (−1)^(i+1) please check](https://www.tinkutara.com/question/Q8109.png)
$${f}\left({x}\right)=\left(\mathrm{1}−{e}^{{x}} \right)^{{n}+\mathrm{1}} \\ $$$$=−\underset{{i}=\mathrm{0}} {\overset{{n}+\mathrm{1}} {\sum}}\:^{{n}+\mathrm{1}} {C}_{{i}} {e}^{{ix}} \left(−\mathrm{1}\right)^{{i}+\mathrm{1}} \\ $$$${f}^{{n}} \left({x}\right)=−\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\:^{{n}+\mathrm{1}} {C}_{{i}} {i}^{{n}} {e}^{{ix}} \left(−\mathrm{1}\right)^{{i}+\mathrm{1}} =\mathrm{required}\:\mathrm{expression} \\ $$$$\mathrm{at}\:{x}=\mathrm{0} \\ $$$$\mathrm{Also}\:{f}\left({x}\right)=\left(\mathrm{1}−{e}^{{x}} \right)^{{n}+\mathrm{1}} ={LHS} \\ $$$${f}\:'\left({x}\right)=−\left({n}+\mathrm{1}\right)\left(\mathrm{1}−{e}^{{x}} \right)^{{n}} \left(−{e}^{{x}} \right) \\ $$$${f}^{\mathrm{2}} \left({x}\right)=−\left[\left({n}+\mathrm{1}\right)\left({e}^{{x}} \right)\left(\mathrm{1}−{e}^{{x}} \right)^{{n}} −\left({n}+\mathrm{1}\right){ne}^{{x}} \left(\mathrm{1}−{e}^{{x}} \right)^{{n}−\mathrm{1}} \left(−{e}^{{x}} \right)\right] \\ $$$$\vdots \\ $$$${f}^{{n}} \left(\mathrm{0}\right)=\mathrm{0}\:\left[\because\left(\mathrm{1}−{e}^{{x}} \right)\:\mathrm{is}\:\mathrm{factor}\:\mathrm{till}\:{n}^{{th}} {differentiation}\right] \\ $$$$\mathrm{hence} \\ $$$$−\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\:^{{n}+\mathrm{1}} {C}_{{i}} {i}^{{n}} \left(−\mathrm{1}\right)^{{i}+\mathrm{1}} \\ $$$$\mathrm{please}\:\mathrm{check} \\ $$
Commented by Yozzia last updated on 30/Sep/16

$${That}\:{seems}\:{sufficient}\:{to}\:{show}\:{that} \\ $$$${the}\:{equation}\:{is}\:{true}.\:{Nicely}\:{done}! \\ $$$${I}\:{like}\:{the}\:{application}\:{of}\:{the}\:{exponential} \\ $$$${function}\:{and}\:{binomial}\:{theorem}. \\ $$
Answered by prakash jain last updated on 22/Sep/16
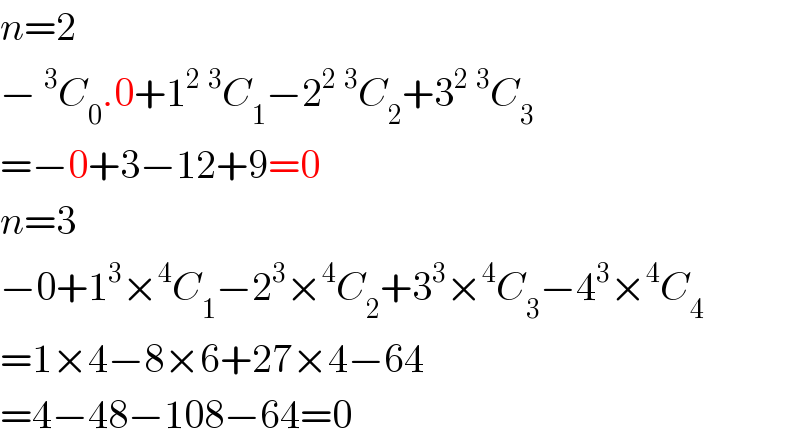
$${n}=\mathrm{2} \\ $$$$−\:^{\mathrm{3}} {C}_{\mathrm{0}} .\mathrm{0}+\mathrm{1}^{\mathrm{2}} \:^{\mathrm{3}} {C}_{\mathrm{1}} −\mathrm{2}^{\mathrm{2}} \:^{\mathrm{3}} {C}_{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \:^{\mathrm{3}} {C}_{\mathrm{3}} \\ $$$$=−\mathrm{0}+\mathrm{3}−\mathrm{12}+\mathrm{9}=\mathrm{0} \\ $$$${n}=\mathrm{3} \\ $$$$−\mathrm{0}+\mathrm{1}^{\mathrm{3}} ×^{\mathrm{4}} {C}_{\mathrm{1}} −\mathrm{2}^{\mathrm{3}} ×^{\mathrm{4}} {C}_{\mathrm{2}} +\mathrm{3}^{\mathrm{3}} ×^{\mathrm{4}} {C}_{\mathrm{3}} −\mathrm{4}^{\mathrm{3}} ×^{\mathrm{4}} {C}_{\mathrm{4}} \\ $$$$=\mathrm{1}×\mathrm{4}−\mathrm{8}×\mathrm{6}+\mathrm{27}×\mathrm{4}−\mathrm{64} \\ $$$$=\mathrm{4}−\mathrm{48}−\mathrm{108}−\mathrm{64}=\mathrm{0} \\ $$
Commented by Yozzia last updated on 22/Sep/16
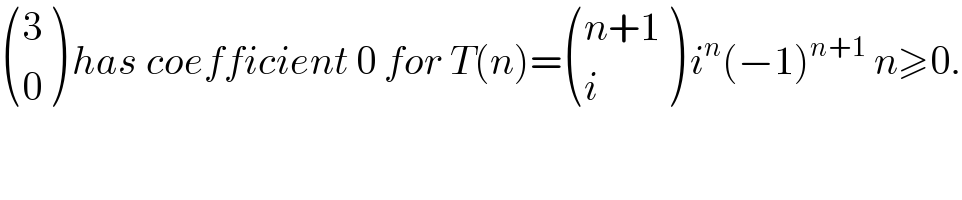
$$\begin{pmatrix}{\mathrm{3}}\\{\mathrm{0}}\end{pmatrix}\:{has}\:{coefficient}\:\mathrm{0}\:{for}\:{T}\left({n}\right)=\begin{pmatrix}{{n}+\mathrm{1}}\\{{i}}\end{pmatrix}\:{i}^{{n}} \left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \:{n}\geqslant\mathrm{0}. \\ $$
Commented by Yozzia last updated on 22/Sep/16

$${I}\:{met}\:{this}\:{series}\:{in}\:{proving}\:{by}\:{induction}\:{that} \\ $$$${the}\:{general}\:{coefficient}\:{a}_{{n}} \:{of}\:{the}\:{terms}\:{in}\:{the}\:{power}\:{series} \\ $$$${of}\:{the}\:{W}−{Lambert}\:{function}\:{is} \\ $$$${a}_{{n}} =\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {n}^{{n}−\mathrm{2}} }{\left({n}−\mathrm{1}\right)!},\:{n}\geqslant\mathrm{1} \\ $$$${W}\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {n}^{{n}−\mathrm{2}} {x}^{{n}} }{\left({n}−\mathrm{1}\right)!}\:\:\:\left\{−\mathrm{1}\leqslant{x}\leqslant\mathrm{1}\right\} \\ $$$${W}\left({x}\right)={f}^{−\mathrm{1}} \left({xe}^{{x}} \right)\:\:{for}\:−\mathrm{1}\leqslant{x}\leqslant\mathrm{1}. \\ $$
Commented by prakash jain last updated on 22/Sep/16
$$\mathrm{Ok}\:\mathrm{my}\:\mathrm{mistake}\:\mathrm{will}\:\mathrm{look}\:\mathrm{at}\:\mathrm{again}. \\ $$
Commented by FilupSmith last updated on 22/Sep/16
$$\mathrm{This}\:\mathrm{is}\:\mathrm{too}\:\mathrm{complicated}.\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know} \\ $$$$\mathrm{much}\:\mathrm{about}\:\mathrm{the}\:{W}−{Function} \\ $$
Commented by prakash jain last updated on 22/Sep/16

$${n}=\mathrm{3}\:{not}\:{zero}. \\ $$
Commented by Yozzia last updated on 22/Sep/16

$${Check}\:{that}\:\mathrm{3}^{\mathrm{3}} \:{term}. \\ $$
Commented by prakash jain last updated on 30/Sep/16
$$\mathrm{Please}\:\mathrm{check}\:\mathrm{answer}\:\mathrm{in}\:\mathrm{comment}.\: \\ $$
