Prove-that-if-p-gt-q-gt-0-and-x-0-then-1-p-x-p-p-1-1-1-q-x-q-q-1-1-

Question Number 1928 by Yozzi last updated on 24/Oct/15

Prove that, if p>q>0 and x≥0, then (1/p)((x^p /(p+1))−1)≥(1/q)((x^q /(q+1))−1).

$${Prove}\:{that},\:{if}\:{p}>{q}>\mathrm{0}\:{and}\:{x}\geqslant\mathrm{0},\:{then} \\ $$$$\:\:\:\:\:\frac{\mathrm{1}}{{p}}\left(\frac{{x}^{{p}} }{{p}+\mathrm{1}}−\mathrm{1}\right)\geqslant\frac{\mathrm{1}}{{q}}\left(\frac{{x}^{{q}} }{{q}+\mathrm{1}}−\mathrm{1}\right).\: \\ $$

Commented by Rasheed Soomro last updated on 24/Oct/15

Prove that, if p>q>0 and x≥0, then (1/p)((x^p /(p+1))−1)≥(1/q)((x^q /(q+1))−1). −−−−−−−−−−−−−−−− A Try. Not much confident Let′s try to achieve simpler equivalent of the given statment,which is easy to prove. Let p=q+k, where k>0 (1/(q+k))((x^(q+k) /(q+k+1))−1)≥(1/q)((x^q /(q+1))−1) (1/(q+k))(((x^(q+k) −q−k−1)/(q+k+1)))≥(1/q)(((x^q −q−1)/(q+1))) ((x^(q+k) −q−k−1)/((q+k)(q+k+1)))≥((x^q −q−1)/(q(q+1))) ((x^(q+k) −q−k−1)/(q^2 +q+2qk+k^2 +k))≥((x^q −q−1)/(q^2 +q)) q>0 ∧ k>0 ⇒ 2qk+k^2 +k>0 Reduction of 2qk+k^2 +k (a +ve number) in the denominator of greater/equal side will leave no effect on the inequality. Hence, ((x^(q+k) −q−k−1)/(q^2 +q))≥((x^q −q−1)/(q^2 +q)) Multiplying by q^2 +q (>0) to both sides x^(q+k) −q−k−1≥x^q −q−1 x^(q+k) −k≥x^q Since k>0 x^(q+k) −k+k≥x^q x^q .x^k ≥x^q Given that x>0 or x=0 for x>0, x^q can be cancelled from both sides: x^k ≥1 Let′s prove for x≥1 first. x^k ≥1 is completely equivalent of the given statement and it is clearly true since x≥1 ∧ k>0 Hence given statement is true for x≥1 For x=0 the result can be proved directly. Now the problem is for x∈(0,1) .... Continue

Commented by prakash jain last updated on 24/Oct/15

Observation on Rasheed Comment ((x^(q+k) −q−k−1)/(q^2 +q+2qk+k^2 +k))≥((x^2 −q−1)/(q^2 +q)) is not equivalent to (if 2qk+k^2 +k>0) ((x^(q+k) −q−k−1)/(q^2 +q))≥((x^2 −q−1)/(q^2 +q)) since ((x^(q+k) −q−k−1)/(q^2 +q+2qk+k^2 +k)) < ((x^(q+k) −q−k−1)/(q^2 +q)) Suggestion: inequality may be simpler to prove if you try p=kq, k>1

$$\mathrm{Observation}\:\mathrm{on}\:\mathrm{Rasheed}\:\mathrm{Comment} \\ $$$$\frac{{x}^{{q}+{k}} −{q}−{k}−\mathrm{1}}{{q}^{\mathrm{2}} +{q}+\mathrm{2}{qk}+{k}^{\mathrm{2}} +{k}}\geqslant\frac{{x}^{\mathrm{2}} −{q}−\mathrm{1}}{{q}^{\mathrm{2}} +{q}} \\ $$$$\mathrm{is}\:\mathrm{not}\:\mathrm{equivalent}\:\mathrm{to}\:\left(\mathrm{if}\:\mathrm{2}{qk}+{k}^{\mathrm{2}} +{k}>\mathrm{0}\right) \\ $$$$\frac{{x}^{{q}+{k}} −{q}−{k}−\mathrm{1}}{{q}^{\mathrm{2}} +{q}}\geqslant\frac{{x}^{\mathrm{2}} −{q}−\mathrm{1}}{{q}^{\mathrm{2}} +{q}} \\ $$$$\:\mathrm{since}\:\frac{{x}^{{q}+{k}} −{q}−{k}−\mathrm{1}}{{q}^{\mathrm{2}} +{q}+\mathrm{2}{qk}+{k}^{\mathrm{2}} +{k}}\:<\:\frac{{x}^{{q}+{k}} −{q}−{k}−\mathrm{1}}{{q}^{\mathrm{2}} +{q}} \\ $$$$\mathrm{Suggestion}:\:\mathrm{inequality}\:\mathrm{may}\:\mathrm{be}\:\mathrm{simpler}\:\mathrm{to}\:\mathrm{prove} \\ $$$$\mathrm{if}\:\mathrm{you}\:\mathrm{try}\:{p}={kq},\:{k}>\mathrm{1} \\ $$

Commented by Rasheed Soomro last updated on 24/Oct/15

THANKSSSSSsss... for correction and suggestion!

$$\boldsymbol{\mathcal{THANKS}\mathrm{S}}\mathrm{S}{SSsss}…\:{for}\:{correction}\:{and}\:{suggestion}! \\ $$

Commented by Rasheed Soomro last updated on 25/Oct/15

Prove that, if p>q>0 and x≥0, then (1/p)((x^p /(p+1))−1)≥(1/q)((x^q /(q+1))−1). −−−−−×××−−−−−−− To get a simpler equivalent(?): (x^p /(p(p+1)))−(1/p)≥(x^q /(q(q+1)))−(1/q)......................(1) Now, p>q ⇒ (1/p)<(1/q) ⇒−(1/p)>−(1/q)..........(2) Adding (1) and (2) (x^p /(p(p+1))) ≥ (x^q /(q(q+1))) Is this equivalent to the original? Does adding a same−sense inequality yield an equivalent inequality? Let p=qk, where k>1 (x^(qk) /(qk(qk+1))) ≥ (x^q /(q(q+1))) (x^(qk) /(k(qk+1))) ≥ (x^q /(q+1)) [Multiplying by q(>0) ] (x^(qk) /(qk^2 +k)) ≥ (x^q /(q+1)) Continue

$${Prove}\:{that},\:{if}\:{p}>{q}>\mathrm{0}\:{and}\:{x}\geqslant\mathrm{0},\:{then} \\ $$$$\:\frac{\mathrm{1}}{{p}}\left(\frac{{x}^{{p}} }{{p}+\mathrm{1}}−\mathrm{1}\right)\geqslant\frac{\mathrm{1}}{{q}}\left(\frac{{x}^{{q}} }{{q}+\mathrm{1}}−\mathrm{1}\right).\: \\ $$$$−−−−−×××−−−−−−− \\ $$$${To}\:{get}\:{a}\:\boldsymbol{\mathrm{simpler}}\:\boldsymbol{\mathrm{equivalent}}\left(?\right): \\ $$$$\frac{{x}^{{p}} }{{p}\left({p}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{p}}\geqslant\frac{{x}^{{q}} }{{q}\left({q}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{q}}………………….\left(\mathrm{1}\right) \\ $$$${Now},\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{p}>{q}\:\Rightarrow\:\frac{\mathrm{1}}{{p}}<\frac{\mathrm{1}}{{q}}\:\Rightarrow−\frac{\mathrm{1}}{{p}}>−\frac{\mathrm{1}}{{q}}……….\left(\mathrm{2}\right) \\ $$$${Adding}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right) \\ $$$$\frac{{x}^{{p}} }{{p}\left({p}+\mathrm{1}\right)}\:\geqslant\:\frac{{x}^{{q}} }{{q}\left({q}+\mathrm{1}\right)} \\ $$$${Is}\:{this}\:{equivalent}\:{to}\:{the}\:{original}? \\ $$$${Does}\:{adding}\:{a}\:\boldsymbol{\mathrm{same}}−\boldsymbol{\mathrm{sense}}\:\boldsymbol{\mathrm{inequality}}\:{yield}\:{an} \\ $$$$\boldsymbol{\mathrm{equivalent}}\:\boldsymbol{\mathrm{inequality}}? \\ $$$${Let}\:{p}={qk},\:{where}\:{k}>\mathrm{1} \\ $$$$\frac{{x}^{{qk}} }{{qk}\left({qk}+\mathrm{1}\right)}\:\geqslant\:\frac{{x}^{{q}} }{{q}\left({q}+\mathrm{1}\right)} \\ $$$$\frac{{x}^{{qk}} }{{k}\left({qk}+\mathrm{1}\right)}\:\geqslant\:\frac{{x}^{{q}} }{{q}+\mathrm{1}}\:\:\:\:\:\:\:\:\:\:\left[{Multiplying}\:{by}\:{q}\left(>\mathrm{0}\right)\:\right] \\ $$$$\frac{{x}^{{qk}} }{{qk}^{\mathrm{2}} +{k}}\:\geqslant\:\frac{{x}^{{q}} }{{q}+\mathrm{1}}\: \\ $$$$ \\ $$$$\boldsymbol{\mathrm{Continue}} \\ $$

Commented by Rasheed Soomro last updated on 25/Oct/15

On the comment of prakash jain Sir you have said that a>b is not equivalent to A>B because (after dropping some +ve value from denominator) A<a. Does this mean a>b and A>B will be equivalent only when A=a?

$$\boldsymbol{\mathrm{On}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{comment}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{prakash}}\:\boldsymbol{\mathrm{jain}} \\ $$$$\boldsymbol{\mathrm{Sir}}\:{you}\:{have}\:{said}\:{that}\:{a}>{b}\:{is}\:{not}\:{equivalent}\:{to}\:{A}>{B} \\ $$$${because}\:\left({after}\:{dropping}\:{some}\:+{ve}\:{value}\:{from}\:{denominator}\right) \\ $$$${A}<{a}. \\ $$$${Does}\:{this}\:{mean}\:{a}>{b}\:{and}\:{A}>{B}\:{will}\:{be}\:{equivalent}\:{only} \\ $$$${when}\:{A}={a}? \\ $$

Commented by prakash jain last updated on 25/Oct/15

While proving if a<A then a>b⇒ A>b but A>b⇏a>b if a>A then A>b⇒a>b but a>b⇏A>b

$$\mathrm{While}\:\mathrm{proving} \\ $$$$\mathrm{if}\:{a}<{A}\:\mathrm{then}\:{a}>{b}\Rightarrow\:{A}>\mathrm{b}\:\mathrm{but}\:{A}>{b}\nRightarrow{a}>{b} \\ $$$$\mathrm{if}\:{a}>{A}\:\mathrm{then}\:{A}>\mathrm{b}\Rightarrow{a}>{b}\:\mathrm{but}\:{a}>{b}\nRightarrow{A}>{b} \\ $$

Commented by prakash jain last updated on 25/Oct/15

Rasheed regarding equality for p>q If (x^p /(p(p+1)))≥(x^q /(q(q+1))) ......(1) then (x^p /(p(p+1)))−(1/p)≥(x^q /(q(q+1))) −(1/q) ......(2) (1) ⇒(2) however (2) does not imply (1). Now you cannot prove 1 since is not true. Try x=1,p=2, q=1

$$\mathrm{Rasheed}\:\mathrm{regarding}\:\mathrm{equality}\:\mathrm{for}\:{p}>{q} \\ $$$$\mathrm{If}\:\frac{{x}^{{p}} }{{p}\left({p}+\mathrm{1}\right)}\geqslant\frac{{x}^{{q}} }{{q}\left({q}+\mathrm{1}\right)}\:\:……\left(\mathrm{1}\right) \\ $$$$\mathrm{then}\:\frac{{x}^{{p}} }{{p}\left({p}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{p}}\geqslant\frac{{x}^{{q}} }{{q}\left({q}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{{q}}\:……\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\:\Rightarrow\left(\mathrm{2}\right)\:\mathrm{however}\:\left(\mathrm{2}\right)\:\mathrm{does}\:\mathrm{not}\:\mathrm{imply}\:\left(\mathrm{1}\right). \\ $$$$\mathrm{Now}\:\mathrm{you}\:\mathrm{cannot}\:\mathrm{prove}\:\mathrm{1}\:\mathrm{since}\:\mathrm{is}\:\mathrm{not}\:\mathrm{true}. \\ $$$$\mathrm{Try}\:{x}=\mathrm{1},{p}=\mathrm{2},\:{q}=\mathrm{1} \\ $$

Commented by Rasheed Soomro last updated on 25/Oct/15

THANKS for so many valueable explanations! However I would like to understand clearly why (x^p /(p(p+1)))−(1/p)≥(x^q /(q(q+1)))−(1/q) does not imply_(−) to (x^p /(p(p+1)))≥(x^q /(q(q+1))) when p>q>0 is also given ? p>q ⇒(1/p)<(1/q)⇒−(1/p)>−(1/q) (x^p /(p(p+1)))−(1/p)≥(x^q /(q(q+1)))−(1/q) ∧ −(1/p)>−(1/q) ⇒(x^p /(p(p+1)))≥(x^q /(q(q+1))) [Subtracting second inequality from first] However as for as equivalence_(−) is concerned I admit that these two are not equivalent.Perhaps this is the reason that one satisfy some values and other not. But since the goal was to determine an equivalent so I failed to achieve. I think implication and equivalence are two different things. Anyway your opinion will be an expert′s opinion and my question is a student′s queztion. I am here to learn from you and other experts.

$$\boldsymbol{\mathcal{THANKS}}\:\boldsymbol{{for}}\:\boldsymbol{{so}}\:\boldsymbol{{many}}\:\boldsymbol{{valueable}}\:\boldsymbol{{explanations}}! \\ $$$$\mathrm{However}\:\mathrm{I}\:\mathrm{would}\:\mathrm{like}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{clearly} \\ $$$$\mathrm{why} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{{x}^{{p}} }{{p}\left({p}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{p}}\geqslant\frac{{x}^{{q}} }{{q}\left({q}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{q}} \\ $$$$\mathrm{does}\:\mathrm{not}\:\underset{−} {\mathrm{imply}}\:\mathrm{to} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{x}^{{p}} }{\mathrm{p}\left({p}+\mathrm{1}\right)}\geqslant\frac{{x}^{{q}} }{\mathrm{q}\left({q}+\mathrm{1}\right)}\:\:\:\: \\ $$$$\mathrm{when}\:\mathrm{p}>\mathrm{q}>\mathrm{0}\:\mathrm{is}\:\mathrm{also}\:\mathrm{given}\:? \\ $$$$\:\:\:\:\:\:\:\:\mathrm{p}>\mathrm{q}\:\Rightarrow\frac{\mathrm{1}}{{p}}<\frac{\mathrm{1}}{{q}}\Rightarrow−\frac{\mathrm{1}}{{p}}>−\frac{\mathrm{1}}{{q}} \\ $$$$\:\:\frac{{x}^{{p}} }{\mathrm{p}\left({p}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{p}}\geqslant\frac{{x}^{{q}} }{\mathrm{q}\left({q}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{q}}\:\wedge\:−\frac{\mathrm{1}}{{p}}>−\frac{\mathrm{1}}{{q}} \\ $$$$\Rightarrow\frac{{x}^{{p}} }{\mathrm{p}\left({p}+\mathrm{1}\right)}\geqslant\frac{{x}^{{q}} }{\mathrm{q}\left({q}+\mathrm{1}\right)}\:\:\left[{Subtracting}\:{second}\:{inequality}\:{from}\:{first}\right] \\ $$$${However}\:{as}\:{for}\:{as}\:\underset{−} {{equivalence}}\:{is}\:{concerned}\:{I}\:{admit} \\ $$$${that}\:\boldsymbol{{these}}\:\boldsymbol{{two}}\:\boldsymbol{{are}}\:\boldsymbol{{not}}\:\boldsymbol{{equivalent}}.{Perhaps}\:{this}\:{is} \\ $$$${the}\:{reason}\:{that}\:{one}\:{satisfy}\:{some}\:{values}\:{and}\:{other}\:{not}. \\ $$$${But}\:{since}\:{the}\:{goal}\:{was}\:{to}\:{determine}\:{an}\:{equivalent}\:{so} \\ $$$$\boldsymbol{{I}}\:\boldsymbol{{failed}}\:\boldsymbol{{to}}\:\boldsymbol{{achieve}}. \\ $$$$\boldsymbol{{I}}\:\boldsymbol{{think}}\:\boldsymbol{{implication}}\:\boldsymbol{{and}}\:\boldsymbol{{equivalence}}\:\boldsymbol{{are}}\:\boldsymbol{{two}} \\ $$$$\boldsymbol{{different}}\:\boldsymbol{{things}}. \\ $$$$\boldsymbol{{Anyway}}\:\boldsymbol{{your}}\:\boldsymbol{{opinion}}\:\boldsymbol{{will}}\:\boldsymbol{{be}}\:\boldsymbol{{an}}\:\boldsymbol{{expert}}'\boldsymbol{{s}}\:\boldsymbol{{opinion}}\: \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{my}}\:\boldsymbol{{question}}\:\boldsymbol{{is}}\:\boldsymbol{{a}}\:\boldsymbol{{student}}'\boldsymbol{{s}}\:\boldsymbol{{queztion}}. \\ $$$$\boldsymbol{{I}}\:\boldsymbol{{am}}\:\boldsymbol{{here}}\:\boldsymbol{{to}}\:\boldsymbol{{learn}}\:\boldsymbol{{from}}\:\boldsymbol{{you}}\:\boldsymbol{{and}}\:\boldsymbol{{other}}\:\boldsymbol{{experts}}. \\ $$$$ \\ $$

Commented by Rasheed Soomro last updated on 27/Oct/15

Prove that, if p>q>0 and x≥0, then (1/p)((x^p /(p+1))−1)≥(1/q)((x^q /(q+1))−1) −×−×−×−×−×−×−×−×−×− (x^p /(p(p+1)))−(1/p)≥(x^q /(q(q+1)))−(1/q) (x^p /(p(p+1)))−(x^q /(q(q+1)))≥(1/p)−(1/q) ((x^p q(q+1)−x^q p(p+1))/(pq(p+1)(q+1)))≥((q−p)/(pq)).....................(A) Approach(1) Let p=qk,where k>1_(−) ((x^p q(q+1)−x^q p(p+1))/(pq(p+1)(q+1)))≥((q−p)/(pq)).....................(A) ((x^(qk) q(q+1)−x^q qk(qk+1))/(q^2 k(qk+1)(q+1)))≥((q−qk)/(q^2 k)) ((x^(qk) q(q+1)−x^q qk(qk+1))/((qk+1)(q+1)))≥q(1−k) ((x^(qk) (q+1)−x^q k(qk+1))/((qk+1)(q+1)))≥1−k ((x^(qk) (q+1)−x^q k(qk+1))/((qk+1)(q+1)))+k≥1 ((x^(qk) (q+1)−x^q k(qk+1)+k(qk+1)(q+1))/((qk+1)(q+1))) ≥ 1 ((x^(qk) q+x^(qk) −x^q qk^2 −x^q k+q^2 k^2 +qk^2 +qk+k)/((qk+1)(q+1)))≥1 ((x^(qk) q+x^(qk) −x^q qk^2 −x^q k+q^2 k^2 +qk^2 +qk+k)/(q^2 k+qk+q+1))≥1 x^(qk) q+x^(qk) −x^q qk^2 −x^q k+q^2 k^2 +qk^2 +qk+k−q^2 k−qk−q−1≥0 ...... Approach(2) Let p=q+k,where k>0 ((x^p q(q+1)−x^q p(p+1))/(pq(p+1)(q+1)))≥((q−p)/(pq)).....................(A) ((x^((q+k)) q(q+1)−x^q (q+k){(q+k)+1})/(q(q+1){(q+k)+1}(q+1)))≥((q−(q+k))/(q(q+k))) ((x^(q+k) q(q+1)−x^q (q+k)(q+k+1))/(q(q+1)^2 (q+k+1)))≥((−k)/(q(q+k))) ((x^(q+k) q(q+1)−x^q (q+k)(q+k+1))/((q+1)^2 (q+k+1)))≥((−k)/(q+k)) [Multiply by q(>0)] ((x^(q+k) q(q+1)−x^q (q+k)(q+k+1))/((q+1)^2 (q+k+1)))+(k/(q+k)) ≥0 (({x^(q+k) q(q+1)−x^q (q+k)(q+k+1)}(q+k)+k(q+1)^2 (q+k+1))/((q+1)^2 (q+k)(q+k+1))) ≥0 Continue

$${Prove}\:{that},\:{if}\:{p}>{q}>\mathrm{0}\:{and}\:{x}\geqslant\mathrm{0},\:{then} \\ $$$$\frac{\mathrm{1}}{{p}}\left(\frac{{x}^{{p}} }{{p}+\mathrm{1}}−\mathrm{1}\right)\geqslant\frac{\mathrm{1}}{{q}}\left(\frac{{x}^{{q}} }{{q}+\mathrm{1}}−\mathrm{1}\right) \\ $$$$−×−×−×−×−×−×−×−×−×− \\ $$$$\frac{{x}^{{p}} }{{p}\left({p}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{p}}\geqslant\frac{{x}^{{q}} }{{q}\left({q}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{q}} \\ $$$$\frac{{x}^{{p}} }{{p}\left({p}+\mathrm{1}\right)}−\frac{{x}^{{q}} }{{q}\left({q}+\mathrm{1}\right)}\geqslant\frac{\mathrm{1}}{{p}}−\frac{\mathrm{1}}{{q}} \\ $$$$\frac{{x}^{{p}} {q}\left({q}+\mathrm{1}\right)−{x}^{{q}} {p}\left({p}+\mathrm{1}\right)}{{pq}\left({p}+\mathrm{1}\right)\left({q}+\mathrm{1}\right)}\geqslant\frac{{q}−{p}}{{pq}}…………………\left({A}\right) \\ $$$${Approach}\left(\mathrm{1}\right) \\ $$$$\underset{−} {{Let}\:{p}={qk},{where}\:{k}>\mathrm{1}} \\ $$$$\frac{{x}^{{p}} {q}\left({q}+\mathrm{1}\right)−{x}^{{q}} {p}\left({p}+\mathrm{1}\right)}{{pq}\left({p}+\mathrm{1}\right)\left({q}+\mathrm{1}\right)}\geqslant\frac{{q}−{p}}{{pq}}…………………\left({A}\right) \\ $$$$\frac{{x}^{{qk}} {q}\left({q}+\mathrm{1}\right)−{x}^{{q}} {qk}\left({qk}+\mathrm{1}\right)}{{q}^{\mathrm{2}} {k}\left({qk}+\mathrm{1}\right)\left({q}+\mathrm{1}\right)}\geqslant\frac{{q}−{qk}}{{q}^{\mathrm{2}} {k}} \\ $$$$\frac{{x}^{{qk}} {q}\left({q}+\mathrm{1}\right)−{x}^{{q}} {qk}\left({qk}+\mathrm{1}\right)}{\left({qk}+\mathrm{1}\right)\left({q}+\mathrm{1}\right)}\geqslant{q}\left(\mathrm{1}−{k}\right) \\ $$$$\frac{{x}^{{qk}} \left({q}+\mathrm{1}\right)−{x}^{{q}} {k}\left({qk}+\mathrm{1}\right)}{\left({qk}+\mathrm{1}\right)\left({q}+\mathrm{1}\right)}\geqslant\mathrm{1}−{k} \\ $$$$\frac{{x}^{{qk}} \left({q}+\mathrm{1}\right)−{x}^{{q}} {k}\left({qk}+\mathrm{1}\right)}{\left({qk}+\mathrm{1}\right)\left({q}+\mathrm{1}\right)}+{k}\geqslant\mathrm{1} \\ $$$$\frac{{x}^{{qk}} \left({q}+\mathrm{1}\right)−{x}^{{q}} {k}\left({qk}+\mathrm{1}\right)+{k}\left({qk}+\mathrm{1}\right)\left({q}+\mathrm{1}\right)}{\left({qk}+\mathrm{1}\right)\left({q}+\mathrm{1}\right)}\:\geqslant\:\mathrm{1} \\ $$$$\frac{{x}^{{qk}} {q}+{x}^{{qk}} −{x}^{{q}} {qk}^{\mathrm{2}} −{x}^{{q}} {k}+{q}^{\mathrm{2}} {k}^{\mathrm{2}} +{qk}^{\mathrm{2}} +{qk}+{k}}{\left({qk}+\mathrm{1}\right)\left({q}+\mathrm{1}\right)}\geqslant\mathrm{1} \\ $$$$\frac{{x}^{{qk}} {q}+{x}^{{qk}} −{x}^{{q}} {qk}^{\mathrm{2}} −{x}^{{q}} {k}+{q}^{\mathrm{2}} {k}^{\mathrm{2}} +{qk}^{\mathrm{2}} +{qk}+{k}}{{q}^{\mathrm{2}} {k}+{qk}+{q}+\mathrm{1}}\geqslant\mathrm{1} \\ $$$${x}^{{qk}} {q}+{x}^{{qk}} −{x}^{{q}} {qk}^{\mathrm{2}} −{x}^{{q}} {k}+{q}^{\mathrm{2}} {k}^{\mathrm{2}} +{qk}^{\mathrm{2}} +{qk}+{k}−{q}^{\mathrm{2}} {k}−{qk}−{q}−\mathrm{1}\geqslant\mathrm{0} \\ $$$$…… \\ $$$${Approach}\left(\mathrm{2}\right) \\ $$$${Let}\:{p}={q}+{k},{where}\:{k}>\mathrm{0} \\ $$$$\frac{{x}^{{p}} {q}\left({q}+\mathrm{1}\right)−{x}^{{q}} {p}\left({p}+\mathrm{1}\right)}{{pq}\left({p}+\mathrm{1}\right)\left({q}+\mathrm{1}\right)}\geqslant\frac{{q}−{p}}{{pq}}…………………\left({A}\right) \\ $$$$\frac{{x}^{\left({q}+{k}\right)} {q}\left({q}+\mathrm{1}\right)−{x}^{{q}} \left({q}+{k}\right)\left\{\left({q}+{k}\right)+\mathrm{1}\right\}}{{q}\left({q}+\mathrm{1}\right)\left\{\left({q}+{k}\right)+\mathrm{1}\right\}\left({q}+\mathrm{1}\right)}\geqslant\frac{{q}−\left({q}+{k}\right)}{{q}\left({q}+{k}\right)} \\ $$$$\frac{{x}^{{q}+{k}} {q}\left({q}+\mathrm{1}\right)−{x}^{{q}} \left({q}+{k}\right)\left({q}+{k}+\mathrm{1}\right)}{{q}\left({q}+\mathrm{1}\right)^{\mathrm{2}} \left({q}+{k}+\mathrm{1}\right)}\geqslant\frac{−{k}}{{q}\left({q}+{k}\right)} \\ $$$$\frac{{x}^{{q}+{k}} {q}\left({q}+\mathrm{1}\right)−{x}^{{q}} \left({q}+{k}\right)\left({q}+{k}+\mathrm{1}\right)}{\left({q}+\mathrm{1}\right)^{\mathrm{2}} \left({q}+{k}+\mathrm{1}\right)}\geqslant\frac{−{k}}{{q}+{k}}\:\:\:\:\left[{Multiply}\:{by}\:{q}\left(>\mathrm{0}\right)\right] \\ $$$$\frac{{x}^{{q}+{k}} {q}\left({q}+\mathrm{1}\right)−{x}^{{q}} \left({q}+{k}\right)\left({q}+{k}+\mathrm{1}\right)}{\left({q}+\mathrm{1}\right)^{\mathrm{2}} \left({q}+{k}+\mathrm{1}\right)}+\frac{{k}}{{q}+{k}}\:\geqslant\mathrm{0}\:\:\: \\ $$$$\frac{\left\{{x}^{{q}+{k}} {q}\left({q}+\mathrm{1}\right)−{x}^{{q}} \left({q}+{k}\right)\left({q}+{k}+\mathrm{1}\right)\right\}\left({q}+{k}\right)+{k}\left({q}+\mathrm{1}\right)^{\mathrm{2}} \left({q}+{k}+\mathrm{1}\right)}{\left({q}+\mathrm{1}\right)^{\mathrm{2}} \left({q}+{k}\right)\left({q}+{k}+\mathrm{1}\right)}\:\geqslant\mathrm{0}\:\:\: \\ $$$${Continue} \\ $$

Commented by Rasheed Soomro last updated on 26/Oct/15

(1/p)((x^p /(p+1))−1)≥(1/q)((x^q /(q+1))−1) p>0,q>0⇒pq>0,multiplying by pq to both sides q((x^p /(p+1))−1)≥p((x^q /(q+1))−1) ((qx^p )/(p+1))−q≥((px^q )/(q+1))−p_ ((qx^p )/(p+1))+p≥((px^q )/(q+1))+q [Adding p+q to both sides] ((qx^p +p(p+1))/(p+1))≥((px^q +q(q+1))/(q+1)) Let p=qk, where k>1 ((qx^(qk) +qk(qk+1))/(qk+1))≥((qkx^q +q(q+1))/(q+1)) q>0 ∧ k>0⇒q+1>0 ∧ qk+1>0 ⇒(qk+1)(q+1)>0 Multiplying by (qk+1)(q+1) to both sides: q{x^(qk) +qk^2 +k}(q+1)≥q{kx^q +q+1}(qk+1) }÷q (>0) {x^(qk) +qk^2 +k}(q+1)≥{kx^q +q+1}(qk+1) qx^(qk) +q^2 k^2 +qk^(×) +x^(qk) +qk^2 +k≥qk^2 x^q +q^2 k+qk^(×) +kx^q +q+1 qx^(qk) +q^2 k^2 +x^(qk) +qk^2 +k≥qk^2 x^q +q^2 k+kx^q +q+1 (q+1)x^(qk) +q^2 k^2 +qk^2 +k≥k(qk+1)x^q +q^2 k+q+1 The above inequality is equivalent to the inequality to be proved.To prove the given it is suficient to prove its equivalent. If we could prove the following inequalities They imply aove inequality. Howdver vice versa is not correct. (q+1)x^(qk) ≥k(qk+1)x^q [.....].....................(i) q^2 k^2 ≥q^2 k⇒(q^2 k)k≥q^2 k [∵ k>1]..........(ii) qk^2 ≥q [k>1 ∧ q>0⇒k^2 >1⇒qk^2 ≥q.....(iii) k≥1 [Assumption]...........................(iv) Unfortinuately (i) is not always correct.For example at x=1 it is false! Dilli hunooz door ast Continue

$$\:\frac{\mathrm{1}}{{p}}\left(\frac{{x}^{{p}} }{{p}+\mathrm{1}}−\mathrm{1}\right)\geqslant\frac{\mathrm{1}}{{q}}\left(\frac{{x}^{{q}} }{{q}+\mathrm{1}}−\mathrm{1}\right) \\ $$$${p}>\mathrm{0},{q}>\mathrm{0}\Rightarrow{pq}>\mathrm{0},{multiplying}\:{by}\:{pq}\:{to}\:{both}\:{sides} \\ $$$$\:{q}\left(\frac{{x}^{{p}} }{{p}+\mathrm{1}}−\mathrm{1}\right)\geqslant{p}\left(\frac{{x}^{{q}} }{{q}+\mathrm{1}}−\mathrm{1}\right) \\ $$$$\:\frac{{qx}^{{p}} }{{p}+\mathrm{1}}−{q}\geqslant\frac{{px}^{{q}} }{{q}+\mathrm{1}}−{p}_{} \\ $$$$\:\frac{{qx}^{{p}} }{{p}+\mathrm{1}}+{p}\geqslant\frac{{px}^{{q}} }{{q}+\mathrm{1}}+{q}\:\:\left[{Adding}\:{p}+{q}\:{to}\:{both}\:{sides}\right] \\ $$$$\:\frac{{qx}^{{p}} +{p}\left({p}+\mathrm{1}\right)}{{p}+\mathrm{1}}\geqslant\frac{{px}^{{q}} +{q}\left({q}+\mathrm{1}\right)}{{q}+\mathrm{1}} \\ $$$${Let}\:{p}={qk},\:{where}\:{k}>\mathrm{1} \\ $$$$\:\frac{{qx}^{{qk}} +{qk}\left({qk}+\mathrm{1}\right)}{{qk}+\mathrm{1}}\geqslant\frac{{qkx}^{{q}} +{q}\left({q}+\mathrm{1}\right)}{{q}+\mathrm{1}} \\ $$$${q}>\mathrm{0}\:\wedge\:{k}>\mathrm{0}\Rightarrow{q}+\mathrm{1}>\mathrm{0}\:\wedge\:{qk}+\mathrm{1}>\mathrm{0}\:\Rightarrow\left({qk}+\mathrm{1}\right)\left({q}+\mathrm{1}\right)>\mathrm{0} \\ $$$${Multiplying}\:{by}\:\left({qk}+\mathrm{1}\right)\left({q}+\mathrm{1}\right)\:{to}\:{both}\:{sides}: \\ $$$$\left.{q}\left\{{x}^{{qk}} +{qk}^{\mathrm{2}} +{k}\right\}\left({q}+\mathrm{1}\right)\geqslant{q}\left\{{kx}^{{q}} +{q}+\mathrm{1}\right\}\left({qk}+\mathrm{1}\right)\:\:\right\}\boldsymbol{\div}{q}\:\left(>\mathrm{0}\right) \\ $$$$\left\{{x}^{{qk}} +{qk}^{\mathrm{2}} +{k}\right\}\left({q}+\mathrm{1}\right)\geqslant\left\{{kx}^{{q}} +{q}+\mathrm{1}\right\}\left({qk}+\mathrm{1}\right) \\ $$$${qx}^{{qk}} +{q}^{\mathrm{2}} {k}^{\mathrm{2}} +\overset{×} {{qk}}+{x}^{{qk}} +{qk}^{\mathrm{2}} +{k}\geqslant{qk}^{\mathrm{2}} {x}^{{q}} +{q}^{\mathrm{2}} {k}+\overset{×} {{qk}}+{kx}^{{q}} +{q}+\mathrm{1} \\ $$$${qx}^{{qk}} +{q}^{\mathrm{2}} {k}^{\mathrm{2}} +{x}^{{qk}} +{qk}^{\mathrm{2}} +{k}\geqslant{qk}^{\mathrm{2}} {x}^{{q}} +{q}^{\mathrm{2}} {k}+{kx}^{{q}} +{q}+\mathrm{1} \\ $$$$\left({q}+\mathrm{1}\right){x}^{{qk}} +{q}^{\mathrm{2}} {k}^{\mathrm{2}} +{qk}^{\mathrm{2}} +{k}\geqslant{k}\left({qk}+\mathrm{1}\right){x}^{{q}} +{q}^{\mathrm{2}} {k}+{q}+\mathrm{1} \\ $$$${The}\:{above}\:{inequality}\:{is}\:{equivalent}\:{to}\:{the}\:{inequality} \\ $$$${to}\:{be}\:{proved}.{To}\:{prove}\:{the}\:{given}\:{it}\:{is}\:{suficient}\:{to} \\ $$$${prove}\:{its}\:{equivalent}. \\ $$$${If}\:{we}\:{could}\:{prove}\:{the}\:{following}\:{inequalities} \\ $$$${They}\:{imply}\:{aove}\:{inequality}.\:{Howdver}\:\:{vice}\:{versa} \\ $$$${is}\:{not}\:{correct}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({q}+\mathrm{1}\right){x}^{{qk}} \geqslant{k}\left({qk}+\mathrm{1}\right){x}^{{q}} \:\:\left[…..\right]…………………\left({i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{q}^{\mathrm{2}} {k}^{\mathrm{2}} \geqslant{q}^{\mathrm{2}} {k}\Rightarrow\left({q}^{\mathrm{2}} {k}\right){k}\geqslant{q}^{\mathrm{2}} {k}\:\left[\because\:{k}>\mathrm{1}\right]……….\left({ii}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{qk}^{\mathrm{2}} \geqslant{q}\:\left[{k}>\mathrm{1}\:\wedge\:{q}>\mathrm{0}\Rightarrow{k}^{\mathrm{2}} >\mathrm{1}\Rightarrow{qk}^{\mathrm{2}} \geqslant{q}…..\left({iii}\right)\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{k}\geqslant\mathrm{1}\:\left[{Assumption}\right]………………………\left({iv}\right) \\ $$$${Unfortinuately}\:\left({i}\right)\:\:{is}\:{not}\:{always}\:{correct}.{For}\:{example} \\ $$$${at}\:{x}=\mathrm{1}\:{it}\:{is}\:{false}! \\ $$$${Dilli}\:{hunooz}\:{door}\:{ast} \\ $$$${Continue} \\ $$

Answered by Rasheed Soomro last updated on 26/Oct/15

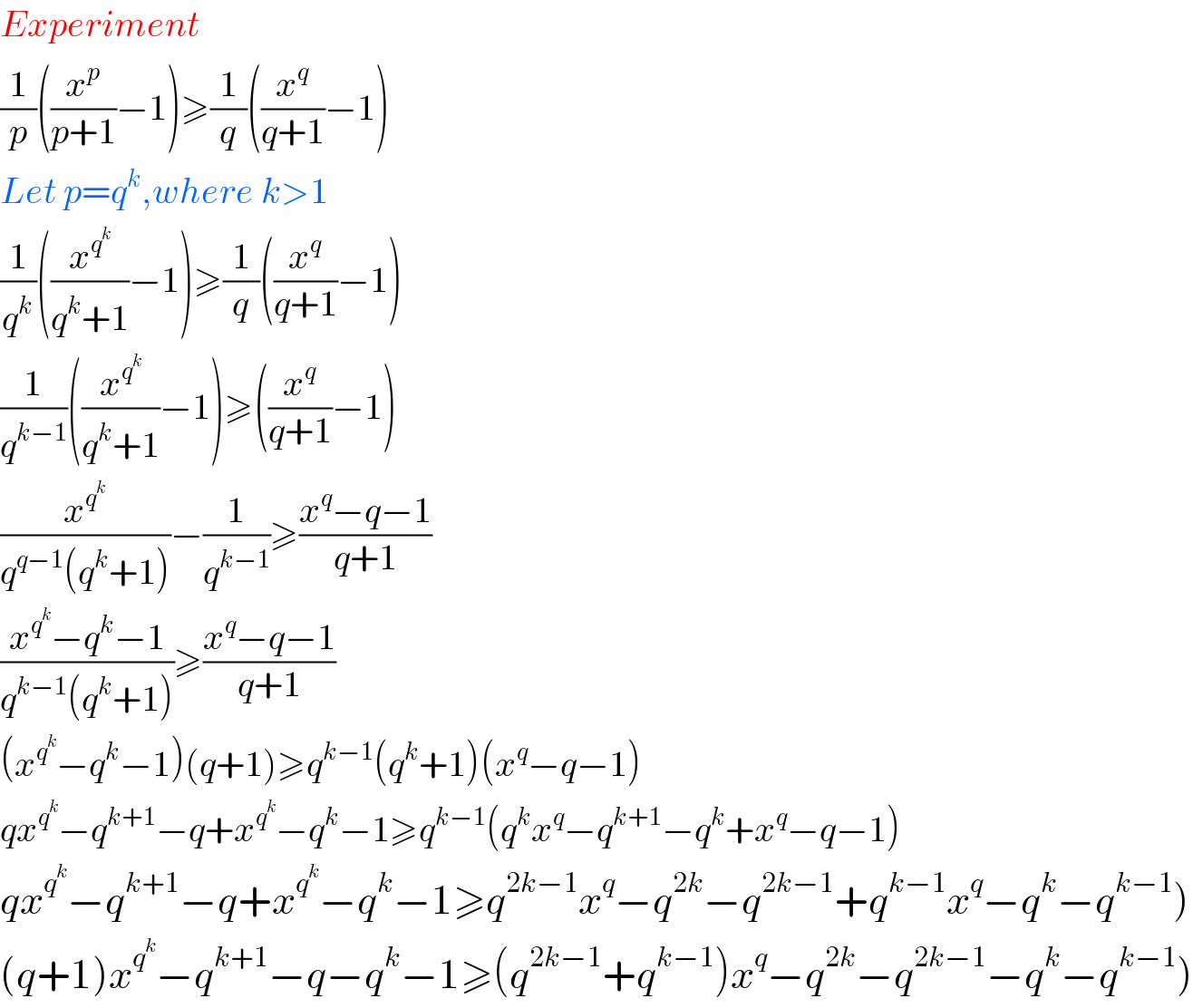
Experiment (1/p)((x^p /(p+1))−1)≥(1/q)((x^q /(q+1))−1) Let p=q^k ,where k>1 (1/q^k )((x^q^k /(q^k +1))−1)≥(1/q)((x^q /(q+1))−1) (1/q^(k−1) )((x^q^k /(q^k +1))−1)≥((x^q /(q+1))−1) (x^q^k /(q^(q−1) (q^k +1)))−(1/q^(k−1) )≥((x^q −q−1)/(q+1)) ((x^q^k −q^k −1)/(q^(k−1) (q^k +1)))≥((x^q −q−1)/(q+1)) (x^q^k −q^k −1)(q+1)≥q^(k−1) (q^k +1)(x^q −q−1) qx^q^k −q^(k+1) −q+x^q^k −q^k −1≥q^(k−1) (q^k x^q −q^(k+1) −q^k +x^q −q−1) qx^q^k −q^(k+1) −q+x^q^k −q^k −1≥q^(2k−1) x^q −q^(2k) −q^(2k−1) +q^(k−1) x^q −q^k −q^(k−1) ) (q+1)x^q^k −q^(k+1) −q−q^k −1≥(q^(2k−1) +q^(k−1) )x^q −q^(2k) −q^(2k−1) −q^k −q^(k−1) )

$${Experiment} \\ $$$$\frac{\mathrm{1}}{{p}}\left(\frac{{x}^{{p}} }{{p}+\mathrm{1}}−\mathrm{1}\right)\geqslant\frac{\mathrm{1}}{{q}}\left(\frac{{x}^{{q}} }{{q}+\mathrm{1}}−\mathrm{1}\right) \\ $$$${Let}\:{p}={q}^{{k}} ,{where}\:{k}>\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{q}^{{k}} }\left(\frac{{x}^{{q}^{{k}} } }{{q}^{{k}} +\mathrm{1}}−\mathrm{1}\right)\geqslant\frac{\mathrm{1}}{{q}}\left(\frac{{x}^{{q}} }{{q}+\mathrm{1}}−\mathrm{1}\right) \\ $$$$\frac{\mathrm{1}}{{q}^{{k}−\mathrm{1}} }\left(\frac{{x}^{{q}^{{k}} } }{{q}^{{k}} +\mathrm{1}}−\mathrm{1}\right)\geqslant\left(\frac{{x}^{{q}} }{{q}+\mathrm{1}}−\mathrm{1}\right) \\ $$$$\frac{{x}^{{q}^{{k}} } }{{q}^{{q}−\mathrm{1}} \left({q}^{{k}} +\mathrm{1}\right)}−\frac{\mathrm{1}}{{q}^{{k}−\mathrm{1}} }\geqslant\frac{{x}^{{q}} −{q}−\mathrm{1}}{{q}+\mathrm{1}} \\ $$$$\frac{{x}^{{q}^{{k}} } −{q}^{{k}} −\mathrm{1}}{{q}^{{k}−\mathrm{1}} \left({q}^{{k}} +\mathrm{1}\right)}\geqslant\frac{{x}^{{q}} −{q}−\mathrm{1}}{{q}+\mathrm{1}} \\ $$$$\left({x}^{{q}^{{k}} } −{q}^{{k}} −\mathrm{1}\right)\left({q}+\mathrm{1}\right)\geqslant{q}^{{k}−\mathrm{1}} \left({q}^{{k}} +\mathrm{1}\right)\left({x}^{{q}} −{q}−\mathrm{1}\right) \\ $$$${qx}^{{q}^{{k}} } −{q}^{{k}+\mathrm{1}} −{q}+{x}^{{q}^{{k}} } −{q}^{{k}} −\mathrm{1}\geqslant{q}^{{k}−\mathrm{1}} \left({q}^{{k}} {x}^{{q}} −{q}^{{k}+\mathrm{1}} −{q}^{{k}} +{x}^{{q}} −{q}−\mathrm{1}\right) \\ $$$$\left.{qx}^{{q}^{{k}} } −{q}^{{k}+\mathrm{1}} −{q}+{x}^{{q}^{{k}} } −{q}^{{k}} −\mathrm{1}\geqslant{q}^{\mathrm{2}{k}−\mathrm{1}} {x}^{{q}} −{q}^{\mathrm{2}{k}} −{q}^{\mathrm{2}{k}−\mathrm{1}} +{q}^{{k}−\mathrm{1}} {x}^{{q}} −{q}^{{k}} −{q}^{{k}−\mathrm{1}} \right) \\ $$$$\left.\left({q}+\mathrm{1}\right){x}^{{q}^{{k}} } −{q}^{{k}+\mathrm{1}} −{q}−{q}^{{k}} −\mathrm{1}\geqslant\left({q}^{\mathrm{2}{k}−\mathrm{1}} +{q}^{{k}−\mathrm{1}} \right){x}^{{q}} −{q}^{\mathrm{2}{k}} −{q}^{\mathrm{2}{k}−\mathrm{1}} −{q}^{{k}} −{q}^{{k}−\mathrm{1}} \right) \\ $$

Answered by Rasheed Soomro last updated on 28/Oct/15

(1/p)((x^p /(p+1))−1)≥(1/q)((x^q /(q+1))−1) (x^p /(p(p+1)))−(1/p)≥(x^q /(q(q+1)))−(1/q) (x^p /(p(p+1)))−(x^q /(q(q+1)))≥(1/p)−(1/q) Let p=qk,where k>1 (x^(qk) /(qk(qk+1)))−(x^q /(q(q+1)))≥(1/(qk))−(1/q) (x^(qk) /(k(qk+1)))−(x^q /((q+1)))≥(1/k)−1 [Multkplying by q(>0)] ((x^(qk) (q+1)−kx^q (qk+1))/(k(q+1)(qk+1)))≥((1−k)/k) ((x^(qk) (q+1)−kx^q (qk+1))/((q+1)(qk+1)))≥1−k [Multiplying by q(>0)] x^(qk) (q+1)−kx^q (qk+1)≥(1−k)(q+1)(qk+1) qx^(ak) +x^(qk) −qk^2 x^q −kx^q ≥(1−k)(q^2 k+q+qk+1) qx^(ak) +x^(qk) −qk^2 x^q −kx^q ≥q^2 k+q+qk^(×) +1−q^2 k^2 −qk^(×) −qk^2 −k qx^(ak) +x^(qk) −qk^2 x^q −kx^q ≥q^2 k+q+1−q^2 k^2 −qk^2 −k

$$\frac{\mathrm{1}}{{p}}\left(\frac{{x}^{{p}} }{{p}+\mathrm{1}}−\mathrm{1}\right)\geqslant\frac{\mathrm{1}}{{q}}\left(\frac{{x}^{{q}} }{{q}+\mathrm{1}}−\mathrm{1}\right) \\ $$$$\frac{{x}^{{p}} }{{p}\left({p}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{p}}\geqslant\frac{{x}^{{q}} }{{q}\left({q}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{q}} \\ $$$$\frac{{x}^{{p}} }{{p}\left({p}+\mathrm{1}\right)}−\frac{{x}^{{q}} }{{q}\left({q}+\mathrm{1}\right)}\geqslant\frac{\mathrm{1}}{{p}}−\frac{\mathrm{1}}{{q}} \\ $$$${Let}\:\:{p}={qk},{where}\:{k}>\mathrm{1} \\ $$$$\frac{{x}^{{qk}} }{{qk}\left({qk}+\mathrm{1}\right)}−\frac{{x}^{{q}} }{{q}\left({q}+\mathrm{1}\right)}\geqslant\frac{\mathrm{1}}{{qk}}−\frac{\mathrm{1}}{{q}} \\ $$$$\frac{{x}^{{qk}} }{{k}\left({qk}+\mathrm{1}\right)}−\frac{{x}^{{q}} }{\left({q}+\mathrm{1}\right)}\geqslant\frac{\mathrm{1}}{{k}}−\mathrm{1}\:\:\:\left[{Multkplying}\:{by}\:{q}\left(>\mathrm{0}\right)\right] \\ $$$$\frac{{x}^{{qk}} \left({q}+\mathrm{1}\right)−{kx}^{{q}} \left({qk}+\mathrm{1}\right)}{{k}\left({q}+\mathrm{1}\right)\left({qk}+\mathrm{1}\right)}\geqslant\frac{\mathrm{1}−{k}}{{k}} \\ $$$$\frac{{x}^{{qk}} \left({q}+\mathrm{1}\right)−{kx}^{{q}} \left({qk}+\mathrm{1}\right)}{\left({q}+\mathrm{1}\right)\left({qk}+\mathrm{1}\right)}\geqslant\mathrm{1}−{k}\:\:\:\:\left[{Multiplying}\:{by}\:{q}\left(>\mathrm{0}\right)\right] \\ $$$${x}^{{qk}} \left({q}+\mathrm{1}\right)−{kx}^{{q}} \left({qk}+\mathrm{1}\right)\geqslant\left(\mathrm{1}−{k}\right)\left({q}+\mathrm{1}\right)\left({qk}+\mathrm{1}\right) \\ $$$${qx}^{{ak}} +{x}^{{qk}} −{qk}^{\mathrm{2}} {x}^{{q}} −{kx}^{{q}} \geqslant\left(\mathrm{1}−{k}\right)\left({q}^{\mathrm{2}} {k}+{q}+{qk}+\mathrm{1}\right) \\ $$$${qx}^{{ak}} +{x}^{{qk}} −{qk}^{\mathrm{2}} {x}^{{q}} −{kx}^{{q}} \geqslant{q}^{\mathrm{2}} {k}+{q}+\overset{×} {{qk}}+\mathrm{1}−{q}^{\mathrm{2}} {k}^{\mathrm{2}} −\overset{×} {{qk}}−{qk}^{\mathrm{2}} −{k} \\ $$$${qx}^{{ak}} +{x}^{{qk}} −{qk}^{\mathrm{2}} {x}^{{q}} −{kx}^{{q}} \geqslant{q}^{\mathrm{2}} {k}+{q}+\mathrm{1}−{q}^{\mathrm{2}} {k}^{\mathrm{2}} −{qk}^{\mathrm{2}} −{k} \\ $$$$ \\ $$$$ \\ $$

Facebook Tweet Pin

Prove-that-if-p-gt-q-gt-0-and-x-0-then-1-p-x-p-p-1-1-1-q-x-q-q-1-1-

Leave a Reply Cancel reply