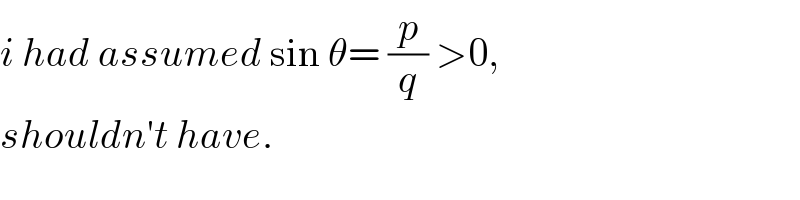Menu Close

prove-that-if-sin-1-x-1-x-then-tan-x-4-2-x-

Tinku Tara 0 Comments
Pin




Question Number 12572 by tawa last updated on 25/Apr/17
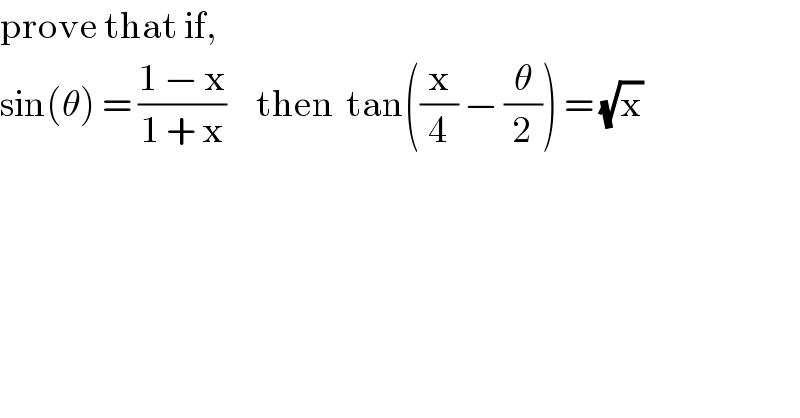
prove that if, sin(θ) = ((1 − x)/(1 + x)) then tan((x/4) − (θ/2)) = (√x)
$$\mathrm{prove}\:\mathrm{that}\:\mathrm{if}, \\ $$$$\mathrm{sin}\left(\theta\right)\:=\:\frac{\mathrm{1}\:−\:\mathrm{x}}{\mathrm{1}\:+\:\mathrm{x}}\:\:\:\:\:\mathrm{then}\:\:\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{4}}\:−\:\frac{\theta}{\mathrm{2}}\right)\:=\:\sqrt{\mathrm{x}} \\ $$
Commented by mrW1 last updated on 26/Apr/17
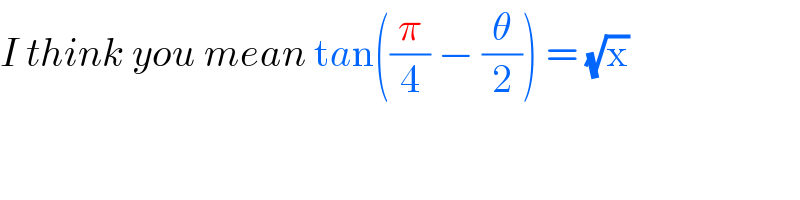
I think you mean tan((π/4) − (θ/2)) = (√x)
$${I}\:{think}\:{you}\:{mean}\:\mathrm{t}{a}\mathrm{n}\left(\frac{\pi}{\mathrm{4}}\:−\:\frac{\theta}{\mathrm{2}}\right)\:=\:\sqrt{\mathrm{x}} \\ $$
Answered by mrW1 last updated on 26/Apr/17
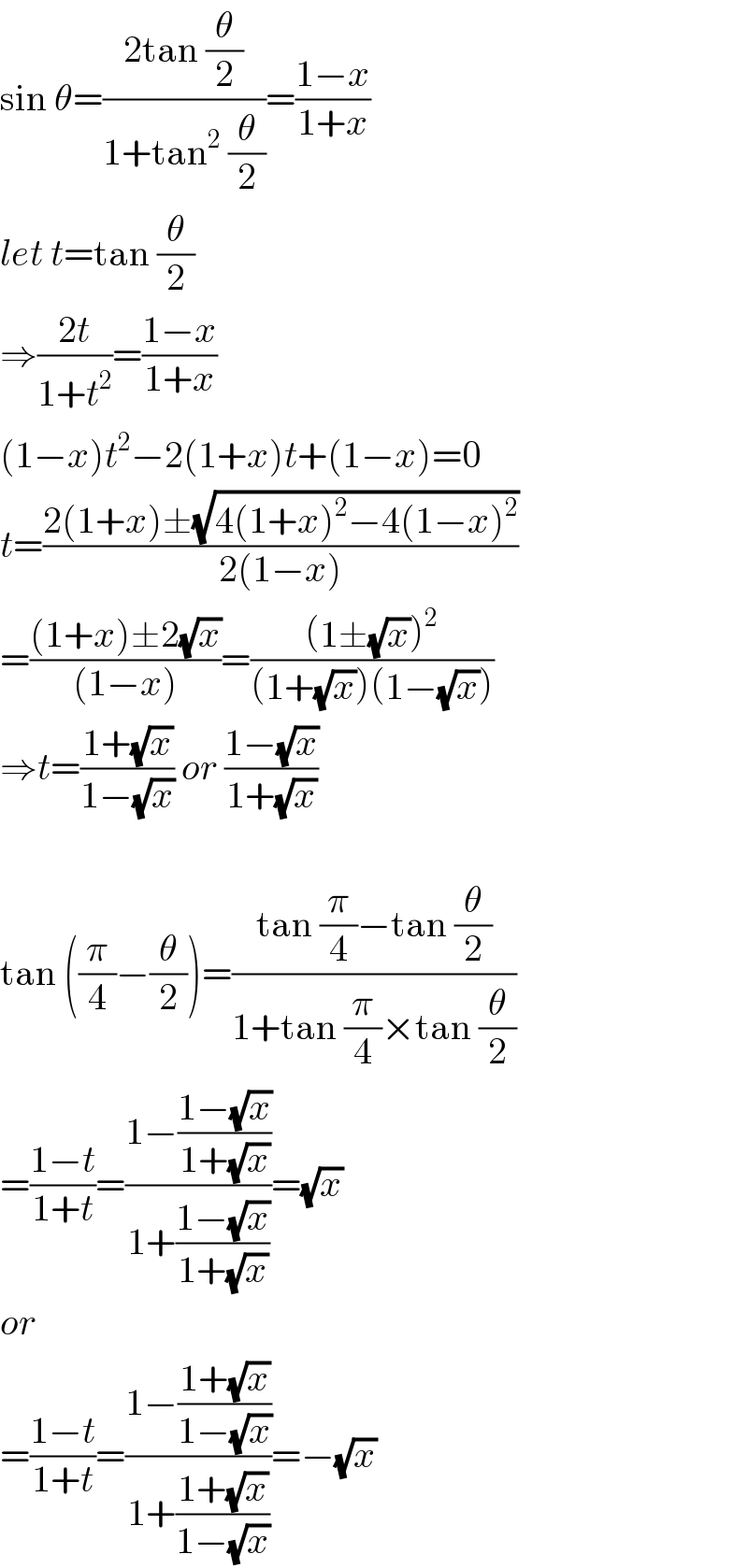
sin θ=((2tan (θ/2))/(1+tan^2 (θ/2)))=((1−x)/(1+x)) let t=tan (θ/2) ⇒((2t)/(1+t^2 ))=((1−x)/(1+x)) (1−x)t^2 −2(1+x)t+(1−x)=0 t=((2(1+x)±(√(4(1+x)^2 −4(1−x)^2 )))/(2(1−x))) =(((1+x)±2(√x))/((1−x)))=(((1±(√x))^2 )/((1+(√x))(1−(√x)))) ⇒t=((1+(√x))/(1−(√x))) or ((1−(√x))/(1+(√x))) tan ((π/4)−(θ/2))=((tan (π/4)−tan (θ/2))/(1+tan (π/4)×tan (θ/2))) =((1−t)/(1+t))=((1−((1−(√x))/(1+(√x))))/(1+((1−(√x))/(1+(√x)))))=(√x) or =((1−t)/(1+t))=((1−((1+(√x))/(1−(√x))))/(1+((1+(√x))/(1−(√x)))))=−(√x)
$$\mathrm{sin}\:\theta=\frac{\mathrm{2tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}=\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}} \\ $$$${let}\:{t}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }=\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}} \\ $$$$\left(\mathrm{1}−{x}\right){t}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}+{x}\right){t}+\left(\mathrm{1}−{x}\right)=\mathrm{0} \\ $$$${t}=\frac{\mathrm{2}\left(\mathrm{1}+{x}\right)\pm\sqrt{\mathrm{4}\left(\mathrm{1}+{x}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }}{\mathrm{2}\left(\mathrm{1}−{x}\right)} \\ $$$$=\frac{\left(\mathrm{1}+{x}\right)\pm\mathrm{2}\sqrt{{x}}}{\left(\mathrm{1}−{x}\right)}=\frac{\left(\mathrm{1}\pm\sqrt{{x}}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\sqrt{{x}}\right)\left(\mathrm{1}−\sqrt{{x}}\right)} \\ $$$$\Rightarrow{t}=\frac{\mathrm{1}+\sqrt{{x}}}{\mathrm{1}−\sqrt{{x}}}\:{or}\:\frac{\mathrm{1}−\sqrt{{x}}}{\mathrm{1}+\sqrt{{x}}} \\ $$$$ \\ $$$$\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)=\frac{\mathrm{tan}\:\frac{\pi}{\mathrm{4}}−\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}\:\frac{\pi}{\mathrm{4}}×\mathrm{tan}\:\frac{\theta}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}=\frac{\mathrm{1}−\frac{\mathrm{1}−\sqrt{{x}}}{\mathrm{1}+\sqrt{{x}}}}{\mathrm{1}+\frac{\mathrm{1}−\sqrt{{x}}}{\mathrm{1}+\sqrt{{x}}}}=\sqrt{{x}} \\ $$$${or} \\ $$$$=\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}=\frac{\mathrm{1}−\frac{\mathrm{1}+\sqrt{{x}}}{\mathrm{1}−\sqrt{{x}}}}{\mathrm{1}+\frac{\mathrm{1}+\sqrt{{x}}}{\mathrm{1}−\sqrt{{x}}}}=−\sqrt{{x}} \\ $$
Commented by tawa last updated on 26/Apr/17
God bless you sir. i really appreciate your effort
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort} \\ $$
Answered by ajfour last updated on 26/Apr/17
tan ((π/4)−(θ/2))=((1−tan (θ/2))/(1+tan (θ/2))) sin θ=((2tan (θ/2))/(1+tan^2 (θ/2)))=((1−x)/(1+x)) =(p/q) (say) ((q−p)/(q+p)) =[((1−tan (θ/2))/(1+tan (θ/2)))]^2 =(((1+x)−(1−x))/((1+x)+(1−x))) ⇒ tan^2 ((π/4)−(θ/2))=((2x)/2) =x ⇒tan ((π/4)−(θ/2))=±(√x) .
$$\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)=\frac{\mathrm{1}−\mathrm{tan}\:\left(\theta/\mathrm{2}\right)}{\mathrm{1}+\mathrm{tan}\:\left(\theta/\mathrm{2}\right)} \\ $$$$\:\:\mathrm{sin}\:\theta=\frac{\mathrm{2tan}\:\left(\theta/\mathrm{2}\right)}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \left(\theta/\mathrm{2}\right)}=\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\:=\frac{{p}}{{q}}\:\left({say}\right) \\ $$$$\frac{{q}−{p}}{{q}+{p}}\:=\left[\frac{\mathrm{1}−\mathrm{tan}\:\left(\theta/\mathrm{2}\right)}{\mathrm{1}+\mathrm{tan}\:\left(\theta/\mathrm{2}\right)}\right]^{\mathrm{2}} \:=\frac{\left(\mathrm{1}+{x}\right)−\left(\mathrm{1}−{x}\right)}{\left(\mathrm{1}+{x}\right)+\left(\mathrm{1}−{x}\right)} \\ $$$$\Rightarrow\:\mathrm{tan}^{\mathrm{2}} \:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)=\frac{\mathrm{2}{x}}{\mathrm{2}}\:={x}\: \\ $$$$\Rightarrow\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)=\pm\sqrt{\boldsymbol{{x}}}\:. \\ $$
Commented by mrW1 last updated on 26/Apr/17
Can you please check: In my way I get tan ((π/4)−(θ/2))=±(√x) but in your way you get only (√(x.)) For example: x=3 sin θ=((1−3)/(1+3))=−(2/4)=−(1/2) ⇒θ=((7π)/6) or −(π/6) (π/4)−(θ/2)=(π/4)−((7π)/(12))=−(π/3) or =(π/4)+(π/(12))=(π/3) tan ((π/4)−(θ/2))=tan (−(π/3))=−(√3) or tan ((π/4)−(θ/2))=tan ((π/3))=(√3) Is something wrong here?
$${Can}\:{you}\:{please}\:{check}: \\ $$$${In}\:{my}\:{way}\:{I}\:{get}\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)=\pm\sqrt{{x}} \\ $$$${but}\:{in}\:{your}\:{way}\:{you}\:{get}\:{only}\:\sqrt{{x}.} \\ $$$$ \\ $$$${For}\:{example}: \\ $$$${x}=\mathrm{3} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{1}−\mathrm{3}}{\mathrm{1}+\mathrm{3}}=−\frac{\mathrm{2}}{\mathrm{4}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\theta=\frac{\mathrm{7}\pi}{\mathrm{6}}\:{or}\:−\frac{\pi}{\mathrm{6}} \\ $$$$\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}=\frac{\pi}{\mathrm{4}}−\frac{\mathrm{7}\pi}{\mathrm{12}}=−\frac{\pi}{\mathrm{3}}\:{or}\:=\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{12}}=\frac{\pi}{\mathrm{3}} \\ $$$$\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)=\mathrm{tan}\:\left(−\frac{\pi}{\mathrm{3}}\right)=−\sqrt{\mathrm{3}} \\ $$$${or} \\ $$$$\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)=\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}\right)=\sqrt{\mathrm{3}} \\ $$$$ \\ $$$${Is}\:{something}\:{wrong}\:{here}? \\ $$
Commented by ajfour last updated on 26/Apr/17
i had assumed sin θ= (p/q) >0, shouldn′t have.
$${i}\:{had}\:{assumed}\:\mathrm{sin}\:\theta=\:\frac{{p}}{{q}}\:>\mathrm{0}, \\ $$$${shouldn}'{t}\:{have}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *