Question Number 6599 by WAI LIN last updated on 05/Jul/16
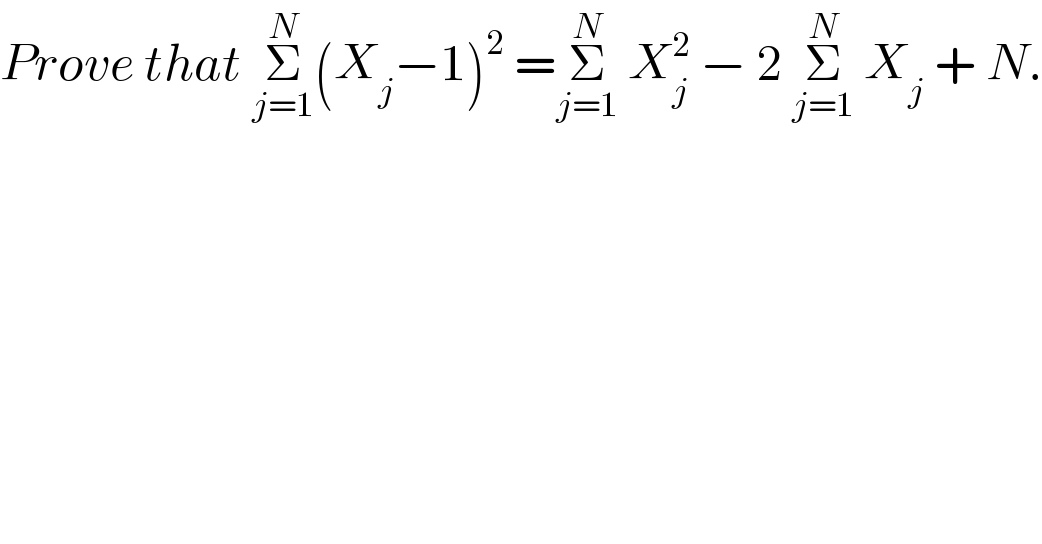
$${Prove}\:{that}\:\underset{{j}=\mathrm{1}} {\overset{{N}} {\sum}}\left({X}_{{j}} −\mathrm{1}\right)^{\mathrm{2}} \:=\underset{{j}=\mathrm{1}} {\overset{{N}} {\sum}}\:{X}_{{j}} ^{\mathrm{2}} \:−\:\mathrm{2}\:\underset{{j}=\mathrm{1}} {\overset{{N}} {\sum}}\:{X}_{{j}} \:+\:{N}. \\ $$
Answered by Temp last updated on 05/Jul/16
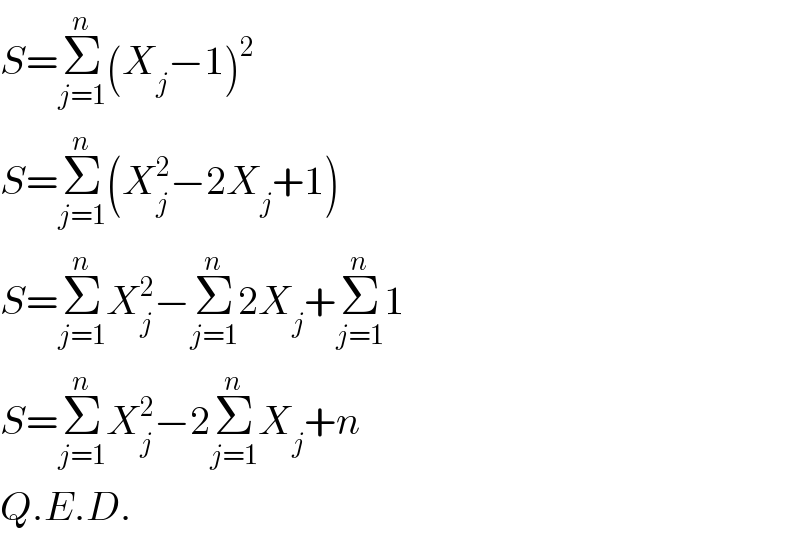
$${S}=\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\left({X}_{{j}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$$${S}=\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\left({X}_{{j}} ^{\mathrm{2}} −\mathrm{2}{X}_{{j}} +\mathrm{1}\right) \\ $$$${S}=\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}{X}_{{j}} ^{\mathrm{2}} −\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{2}{X}_{{j}} +\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{1} \\ $$$${S}=\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}{X}_{{j}} ^{\mathrm{2}} −\mathrm{2}\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}{X}_{{j}} +{n} \\ $$$${Q}.{E}.{D}. \\ $$
Commented by WAI LIN last updated on 05/Jul/16

$${Thank}! \\ $$
