Question Number 73590 by mhmd last updated on 13/Nov/19
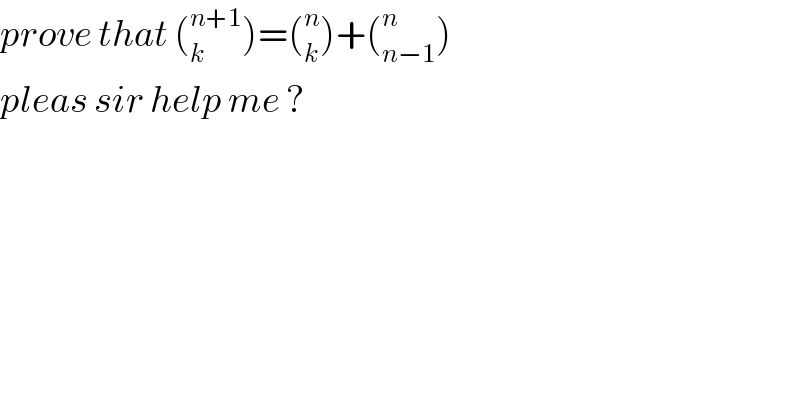
$${prove}\:{that}\:\left(_{{k}} ^{{n}+\mathrm{1}} \right)=\left(_{{k}} ^{{n}} \right)+\left(_{{n}−\mathrm{1}} ^{{n}} \right) \\ $$$${pleas}\:{sir}\:{help}\:{me}\:? \\ $$
Commented by Cmr 237 last updated on 13/Nov/19
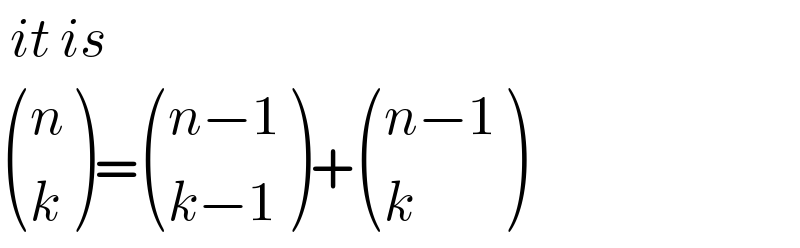
$$\:{it}\:{is} \\ $$$$\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}=\begin{pmatrix}{{n}−\mathrm{1}}\\{{k}−\mathrm{1}}\end{pmatrix}+\begin{pmatrix}{{n}−\mathrm{1}}\\{{k}}\end{pmatrix} \\ $$
Commented by mathmax by abdo last updated on 13/Nov/19
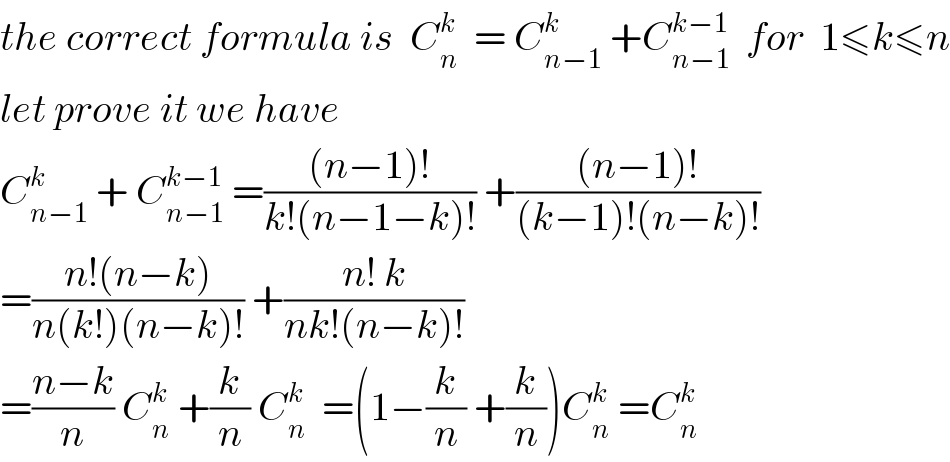
$${the}\:{correct}\:{formula}\:{is}\:\:{C}_{{n}} ^{{k}} \:\:=\:{C}_{{n}−\mathrm{1}} ^{{k}} \:+{C}_{{n}−\mathrm{1}} ^{{k}−\mathrm{1}} \:\:{for}\:\:\mathrm{1}\leqslant{k}\leqslant{n} \\ $$$${let}\:{prove}\:{it}\:{we}\:{have} \\ $$$${C}_{{n}−\mathrm{1}} ^{{k}} \:+\:{C}_{{n}−\mathrm{1}} ^{{k}−\mathrm{1}} \:=\frac{\left({n}−\mathrm{1}\right)!}{{k}!\left({n}−\mathrm{1}−{k}\right)!}\:+\frac{\left({n}−\mathrm{1}\right)!}{\left({k}−\mathrm{1}\right)!\left({n}−{k}\right)!} \\ $$$$=\frac{{n}!\left({n}−{k}\right)}{{n}\left({k}!\right)\left({n}−{k}\right)!}\:+\frac{{n}!\:{k}}{{nk}!\left({n}−{k}\right)!} \\ $$$$=\frac{{n}−{k}}{{n}}\:{C}_{{n}} ^{{k}} \:+\frac{{k}}{{n}}\:{C}_{{n}} ^{{k}} \:\:=\left(\mathrm{1}−\frac{{k}}{{n}}\:+\frac{{k}}{{n}}\right){C}_{{n}} ^{{k}} \:={C}_{{n}} ^{{k}} \\ $$
Answered by Cmr 237 last updated on 13/Nov/19
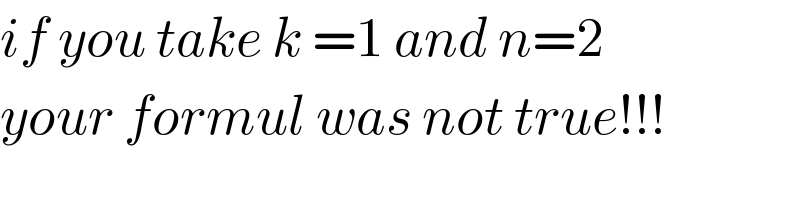
$${if}\:{you}\:{take}\:{k}\:=\mathrm{1}\:{and}\:{n}=\mathrm{2} \\ $$$${your}\:{formul}\:{was}\:{not}\:{true}!!! \\ $$
Answered by malwaan last updated on 14/Nov/19
![((n),(k) ) + ((n),((k−1)) ) = ((n!)/(k!(n−k)!)) + ((n!)/((k−1)!(n−k+1)!)) = ((n!)/(k(k−1)!(n−k)!)) + ((n!)/((k−1)!(n−k+1)(n−k)!)) = ((n![(n−k+1)+k])/(k(k−1)!(n−k+1)(n−k)!)) =((n!(n+1))/(k!(n−k+1)!))=(((n+1)!)/(k![(n+1)−k]!)) = (((n+1)),(k) )](https://www.tinkutara.com/question/Q73629.png)
$$\begin{pmatrix}{\boldsymbol{{n}}}\\{\boldsymbol{{k}}}\end{pmatrix}\:+\begin{pmatrix}{\boldsymbol{{n}}}\\{\boldsymbol{{k}}−\mathrm{1}}\end{pmatrix}\:= \\ $$$$\frac{\boldsymbol{{n}}!}{\boldsymbol{{k}}!\left(\boldsymbol{{n}}−\boldsymbol{{k}}\right)!}\:+\:\frac{\boldsymbol{{n}}!}{\left(\boldsymbol{{k}}−\mathrm{1}\right)!\left(\boldsymbol{{n}}−\boldsymbol{{k}}+\mathrm{1}\right)!} \\ $$$$=\:\:\frac{\boldsymbol{{n}}!}{\boldsymbol{{k}}\left(\boldsymbol{{k}}−\mathrm{1}\right)!\left(\boldsymbol{{n}}−\boldsymbol{{k}}\right)!}\:+ \\ $$$$\:\:\:\:\:\:\frac{\boldsymbol{{n}}!}{\left(\boldsymbol{{k}}−\mathrm{1}\right)!\left(\boldsymbol{{n}}−\boldsymbol{{k}}+\mathrm{1}\right)\left(\boldsymbol{{n}}−\boldsymbol{{k}}\right)!} \\ $$$$=\:\frac{\boldsymbol{{n}}!\left[\left(\boldsymbol{{n}}−\boldsymbol{{k}}+\mathrm{1}\right)+\boldsymbol{{k}}\right]}{\boldsymbol{{k}}\left(\boldsymbol{{k}}−\mathrm{1}\right)!\left(\boldsymbol{{n}}−\boldsymbol{{k}}+\mathrm{1}\right)\left(\boldsymbol{{n}}−\boldsymbol{{k}}\right)!} \\ $$$$=\frac{\boldsymbol{{n}}!\left(\boldsymbol{{n}}+\mathrm{1}\right)}{\boldsymbol{{k}}!\left(\boldsymbol{{n}}−\boldsymbol{{k}}+\mathrm{1}\right)!}=\frac{\left(\boldsymbol{{n}}+\mathrm{1}\right)!}{\boldsymbol{{k}}!\left[\left(\boldsymbol{{n}}+\mathrm{1}\right)−\boldsymbol{{k}}\right]!} \\ $$$$=\:\begin{pmatrix}{\boldsymbol{{n}}+\mathrm{1}}\\{\boldsymbol{{k}}}\end{pmatrix} \\ $$
