Question Number 8839 by tawakalitu last updated on 31/Oct/16
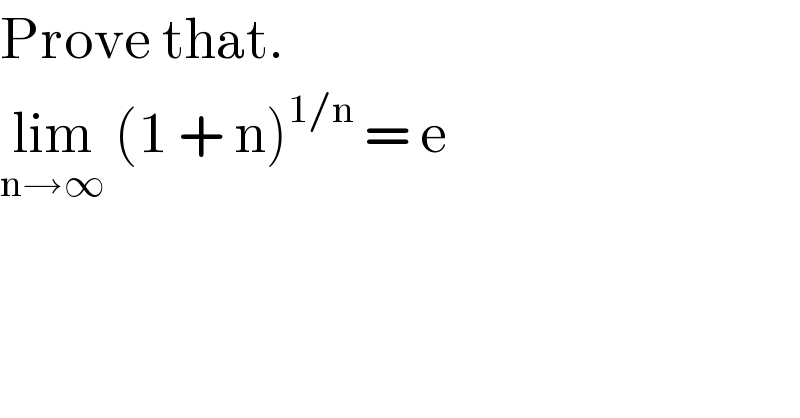
$$\mathrm{Prove}\:\mathrm{that}.\: \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}\:+\:\mathrm{n}\right)^{\mathrm{1}/\mathrm{n}} \:=\:\mathrm{e} \\ $$
Answered by FilupSmith last updated on 31/Oct/16
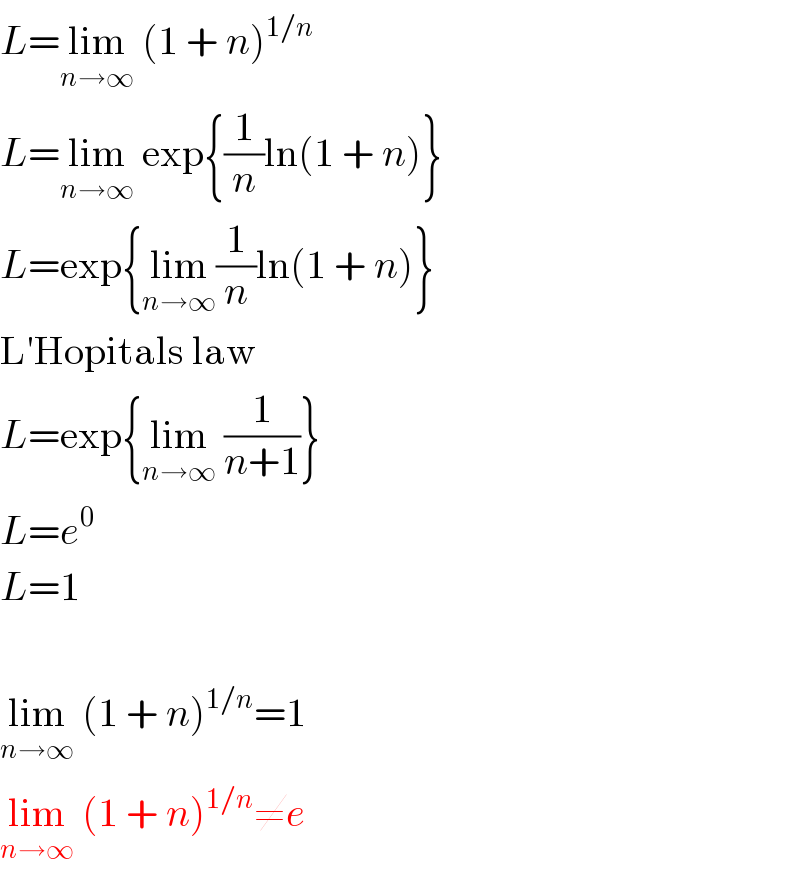
$${L}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}\:+\:{n}\right)^{\mathrm{1}/{n}} \\ $$$${L}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{exp}\left\{\frac{\mathrm{1}}{{n}}\mathrm{ln}\left(\mathrm{1}\:+\:{n}\right)\right\} \\ $$$${L}=\mathrm{exp}\left\{\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\mathrm{ln}\left(\mathrm{1}\:+\:{n}\right)\right\} \\ $$$$\mathrm{L}'\mathrm{Hopitals}\:\mathrm{law} \\ $$$${L}=\mathrm{exp}\left\{\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{{n}+\mathrm{1}}\right\} \\ $$$${L}={e}^{\mathrm{0}} \\ $$$${L}=\mathrm{1} \\ $$$$ \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}\:+\:{n}\right)^{\mathrm{1}/{n}} =\mathrm{1} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}\:+\:{n}\right)^{\mathrm{1}/{n}} \neq{e} \\ $$
Commented by tawakalitu last updated on 31/Oct/16
$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
