Menu Close

Prove-that-m-N-r-1-m-2m-2r-1-2r-1-2m-1-r-1-m-2m-2r-2r-2m-1-

Tinku Tara 0 Comments
Pin




Question Number 8013 by Yozzia last updated on 28/Sep/16
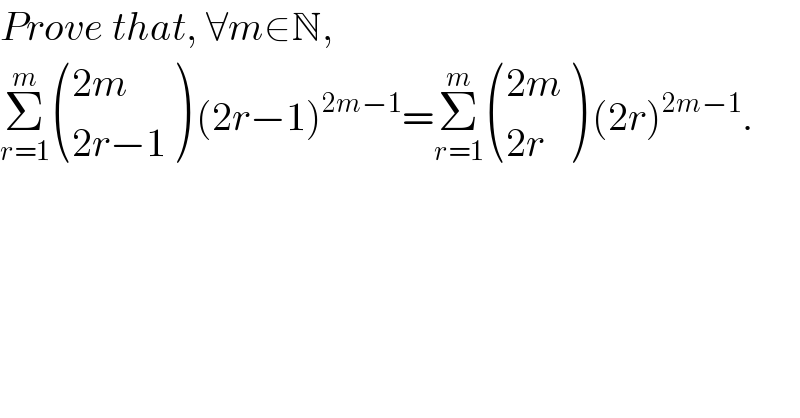
Prove that, ∀m∈N, Σ_(r=1) ^m (((2m)),((2r−1)) ) (2r−1)^(2m−1) =Σ_(r=1) ^m (((2m)),((2r)) ) (2r)^(2m−1) .
$${Prove}\:{that},\:\forall{m}\in\mathbb{N}, \\ $$$$\underset{{r}=\mathrm{1}} {\overset{{m}} {\sum}}\begin{pmatrix}{\mathrm{2}{m}}\\{\mathrm{2}{r}−\mathrm{1}}\end{pmatrix}\:\left(\mathrm{2}{r}−\mathrm{1}\right)^{\mathrm{2}{m}−\mathrm{1}} =\underset{{r}=\mathrm{1}} {\overset{{m}} {\sum}}\begin{pmatrix}{\mathrm{2}{m}}\\{\mathrm{2}{r}}\end{pmatrix}\:\left(\mathrm{2}{r}\right)^{\mathrm{2}{m}−\mathrm{1}} . \\ $$
Commented by FilupSmith last updated on 28/Sep/16
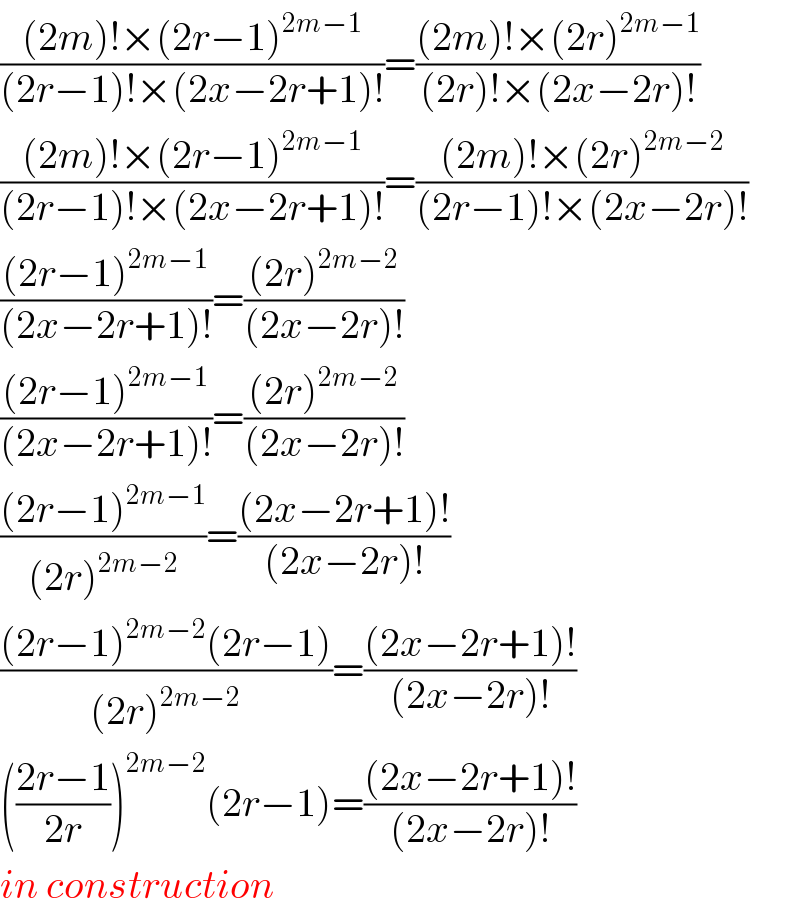
(((2m)!×(2r−1)^(2m−1) )/((2r−1)!×(2x−2r+1)!))=(((2m)!×(2r)^(2m−1) )/((2r)!×(2x−2r)!)) (((2m)!×(2r−1)^(2m−1) )/((2r−1)!×(2x−2r+1)!))=(((2m)!×(2r)^(2m−2) )/((2r−1)!×(2x−2r)!)) (((2r−1)^(2m−1) )/((2x−2r+1)!))=(((2r)^(2m−2) )/((2x−2r)!)) (((2r−1)^(2m−1) )/((2x−2r+1)!))=(((2r)^(2m−2) )/((2x−2r)!)) (((2r−1)^(2m−1) )/((2r)^(2m−2) ))=(((2x−2r+1)!)/((2x−2r)!)) (((2r−1)^(2m−2) (2r−1))/((2r)^(2m−2) ))=(((2x−2r+1)!)/((2x−2r)!)) (((2r−1)/(2r)))^(2m−2) (2r−1)=(((2x−2r+1)!)/((2x−2r)!)) in construction
$$\frac{\left(\mathrm{2}{m}\right)!×\left(\mathrm{2}{r}−\mathrm{1}\right)^{\mathrm{2}{m}−\mathrm{1}} }{\left(\mathrm{2}{r}−\mathrm{1}\right)!×\left(\mathrm{2}{x}−\mathrm{2}{r}+\mathrm{1}\right)!}=\frac{\left(\mathrm{2}{m}\right)!×\left(\mathrm{2}{r}\right)^{\mathrm{2}{m}−\mathrm{1}} }{\left(\mathrm{2}{r}\right)!×\left(\mathrm{2}{x}−\mathrm{2}{r}\right)!} \\ $$$$\frac{\left(\mathrm{2}{m}\right)!×\left(\mathrm{2}{r}−\mathrm{1}\right)^{\mathrm{2}{m}−\mathrm{1}} }{\left(\mathrm{2}{r}−\mathrm{1}\right)!×\left(\mathrm{2}{x}−\mathrm{2}{r}+\mathrm{1}\right)!}=\frac{\left(\mathrm{2}{m}\right)!×\left(\mathrm{2}{r}\right)^{\mathrm{2}{m}−\mathrm{2}} }{\left(\mathrm{2}{r}−\mathrm{1}\right)!×\left(\mathrm{2}{x}−\mathrm{2}{r}\right)!} \\ $$$$\frac{\left(\mathrm{2}{r}−\mathrm{1}\right)^{\mathrm{2}{m}−\mathrm{1}} }{\left(\mathrm{2}{x}−\mathrm{2}{r}+\mathrm{1}\right)!}=\frac{\left(\mathrm{2}{r}\right)^{\mathrm{2}{m}−\mathrm{2}} }{\left(\mathrm{2}{x}−\mathrm{2}{r}\right)!} \\ $$$$\frac{\left(\mathrm{2}{r}−\mathrm{1}\right)^{\mathrm{2}{m}−\mathrm{1}} }{\left(\mathrm{2}{x}−\mathrm{2}{r}+\mathrm{1}\right)!}=\frac{\left(\mathrm{2}{r}\right)^{\mathrm{2}{m}−\mathrm{2}} }{\left(\mathrm{2}{x}−\mathrm{2}{r}\right)!} \\ $$$$\frac{\left(\mathrm{2}{r}−\mathrm{1}\right)^{\mathrm{2}{m}−\mathrm{1}} }{\left(\mathrm{2}{r}\right)^{\mathrm{2}{m}−\mathrm{2}} }=\frac{\left(\mathrm{2}{x}−\mathrm{2}{r}+\mathrm{1}\right)!}{\left(\mathrm{2}{x}−\mathrm{2}{r}\right)!} \\ $$$$\frac{\left(\mathrm{2}{r}−\mathrm{1}\right)^{\mathrm{2}{m}−\mathrm{2}} \left(\mathrm{2}{r}−\mathrm{1}\right)}{\left(\mathrm{2}{r}\right)^{\mathrm{2}{m}−\mathrm{2}} }=\frac{\left(\mathrm{2}{x}−\mathrm{2}{r}+\mathrm{1}\right)!}{\left(\mathrm{2}{x}−\mathrm{2}{r}\right)!} \\ $$$$\left(\frac{\mathrm{2}{r}−\mathrm{1}}{\mathrm{2}{r}}\right)^{\mathrm{2}{m}−\mathrm{2}} \left(\mathrm{2}{r}−\mathrm{1}\right)=\frac{\left(\mathrm{2}{x}−\mathrm{2}{r}+\mathrm{1}\right)!}{\left(\mathrm{2}{x}−\mathrm{2}{r}\right)!} \\ $$$${in}\:{construction} \\ $$
Commented by prakash jain last updated on 30/Sep/16
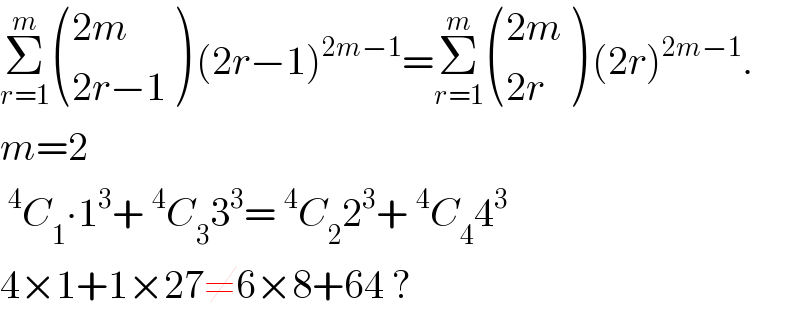
Σ_(r=1) ^m (((2m)),((2r−1)) ) (2r−1)^(2m−1) =Σ_(r=1) ^m (((2m)),((2r)) ) (2r)^(2m−1) . m=2 ^4 C_1 ∙1^3 +^4 C_3 3^3 =^4 C_2 2^3 +^4 C_4 4^3 4×1+1×27≠6×8+64 ?
$$\underset{{r}=\mathrm{1}} {\overset{{m}} {\sum}}\begin{pmatrix}{\mathrm{2}{m}}\\{\mathrm{2}{r}−\mathrm{1}}\end{pmatrix}\:\left(\mathrm{2}{r}−\mathrm{1}\right)^{\mathrm{2}{m}−\mathrm{1}} =\underset{{r}=\mathrm{1}} {\overset{{m}} {\sum}}\begin{pmatrix}{\mathrm{2}{m}}\\{\mathrm{2}{r}}\end{pmatrix}\:\left(\mathrm{2}{r}\right)^{\mathrm{2}{m}−\mathrm{1}} . \\ $$$${m}=\mathrm{2} \\ $$$$\:^{\mathrm{4}} {C}_{\mathrm{1}} \centerdot\mathrm{1}^{\mathrm{3}} +\:^{\mathrm{4}} {C}_{\mathrm{3}} \mathrm{3}^{\mathrm{3}} =\:^{\mathrm{4}} {C}_{\mathrm{2}} \mathrm{2}^{\mathrm{3}} +\:^{\mathrm{4}} {C}_{\mathrm{4}} \mathrm{4}^{\mathrm{3}} \\ $$$$\mathrm{4}×\mathrm{1}+\mathrm{1}×\mathrm{27}\neq\mathrm{6}×\mathrm{8}+\mathrm{64}\:? \\ $$
Commented by Yozzia last updated on 30/Sep/16
4×1+4×27=6×8+64
$$\mathrm{4}×\mathrm{1}+\mathrm{4}×\mathrm{27}=\mathrm{6}×\mathrm{8}+\mathrm{64} \\ $$
Commented by prakash jain last updated on 30/Sep/16
Ok. I made this error so many times.
$$\mathrm{O}{k}.\:\mathrm{I}\:\mathrm{made}\:\mathrm{this}\:\mathrm{error}\:\mathrm{so}\:\mathrm{many}\:\mathrm{times}. \\ $$
Answered by prakash jain last updated on 01/Oct/16
(1−e^x )^(2m) =Σ_(k=0) ^(2m) ^(2m) C_k e^(kx) (−1)^k Let us write C_k for^(2m) C_k (d^(2m−1) /dx^(2m−1) )(1−e^x )^(2m) =Σ_(k=1) ^(2m) ^(2m) C_k k^(2m−1) (−1)^k index start from 1 since k=0 is a constant with derivative 0. LHS is 0 at x=0 since (1−e^x ) will be factor. RHS −C_1 (1)^(2m−1) +C_2 (2)^(2m−1) +−..+C_(2m) (2m)^(2m−1) =0 ⇒Σ_(r=1) ^m C_(2r) (2r)^(2m−1) =Σ_(r=1) ^m C_(2r−1) (2r−1)^(2m−1) odd terms equal to even term (excep C_0 )
$$\left(\mathrm{1}−{e}^{{x}} \right)^{\mathrm{2}{m}} =\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{m}} {\sum}}\:^{\mathrm{2}{m}} {C}_{{k}} {e}^{{kx}} \left(−\mathrm{1}\right)^{{k}} \\ $$$$\mathrm{Let}\:\mathrm{us}\:\mathrm{write}\:{C}_{{k}} \:{for}\:^{\mathrm{2}{m}} {C}_{{k}} \\ $$$$\frac{{d}^{\mathrm{2}{m}−\mathrm{1}} }{{dx}^{\mathrm{2}{m}−\mathrm{1}} }\left(\mathrm{1}−{e}^{{x}} \right)^{\mathrm{2}{m}} =\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{m}} {\sum}}\:^{\mathrm{2}{m}} {C}_{{k}} {k}^{\mathrm{2}{m}−\mathrm{1}} \left(−\mathrm{1}\right)^{{k}} \\ $$$$\mathrm{index}\:\mathrm{start}\:\mathrm{from}\:\mathrm{1}\:\mathrm{since}\:{k}=\mathrm{0}\:\mathrm{is}\:\mathrm{a}\:\mathrm{constant}\: \\ $$$$\mathrm{with}\:\mathrm{derivative}\:\mathrm{0}. \\ $$$$\mathrm{LHS}\:\mathrm{is}\:\mathrm{0}\:{at}\:{x}=\mathrm{0}\:\mathrm{since}\:\left(\mathrm{1}−{e}^{{x}} \right)\:\mathrm{will}\:\mathrm{be}\:\mathrm{factor}. \\ $$$$\mathrm{RHS} \\ $$$$−{C}_{\mathrm{1}} \left(\mathrm{1}\right)^{\mathrm{2}{m}−\mathrm{1}} +{C}_{\mathrm{2}} \left(\mathrm{2}\right)^{\mathrm{2}{m}−\mathrm{1}} +−..+{C}_{\mathrm{2}{m}} \left(\mathrm{2}{m}\right)^{\mathrm{2}{m}−\mathrm{1}} =\mathrm{0} \\ $$$$\Rightarrow\underset{{r}=\mathrm{1}} {\overset{{m}} {\sum}}{C}_{\mathrm{2}{r}} \left(\mathrm{2}{r}\right)^{\mathrm{2}{m}−\mathrm{1}} =\underset{{r}=\mathrm{1}} {\overset{{m}} {\sum}}{C}_{\mathrm{2}{r}−\mathrm{1}} \left(\mathrm{2}{r}−\mathrm{1}\right)^{\mathrm{2}{m}−\mathrm{1}} \\ $$$$\mathrm{odd}\:\mathrm{terms}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{even}\:\mathrm{term}\:\left(\mathrm{excep}\:\mathrm{C}_{\mathrm{0}} \right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *