Question Number 2340 by Yozzi last updated on 18/Nov/15
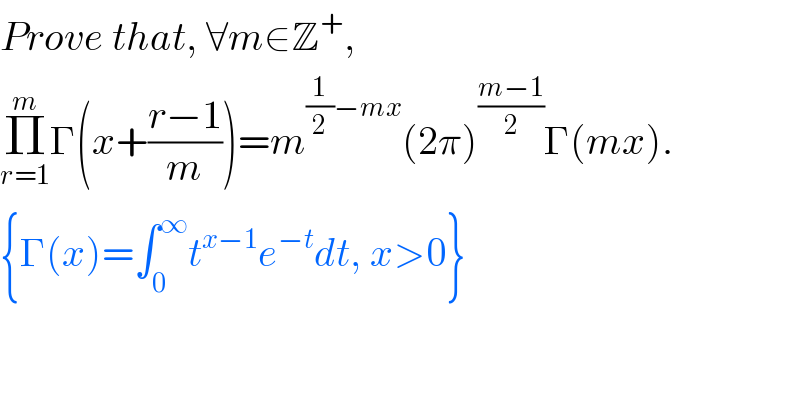
$${Prove}\:{that},\:\forall{m}\in\mathbb{Z}^{+} , \\ $$$$\underset{{r}=\mathrm{1}} {\overset{{m}} {\prod}}\Gamma\left({x}+\frac{{r}−\mathrm{1}}{{m}}\right)={m}^{\frac{\mathrm{1}}{\mathrm{2}}−{mx}} \left(\mathrm{2}\pi\right)^{\frac{{m}−\mathrm{1}}{\mathrm{2}}} \Gamma\left({mx}\right). \\ $$$$\left\{\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{x}−\mathrm{1}} {e}^{−{t}} {dt},\:{x}>\mathrm{0}\right\} \\ $$
Commented by prakash jain last updated on 18/Nov/15
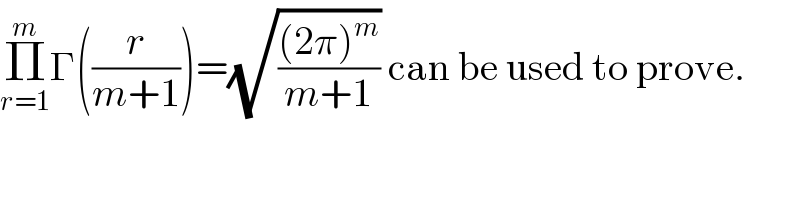
$$\underset{{r}=\mathrm{1}} {\overset{{m}} {\prod}}\Gamma\left(\frac{{r}}{{m}+\mathrm{1}}\right)=\sqrt{\frac{\left(\mathrm{2}\pi\right)^{{m}} }{{m}+\mathrm{1}}}\:\mathrm{can}\:\mathrm{be}\:\mathrm{used}\:\mathrm{to}\:\mathrm{prove}. \\ $$$$ \\ $$
