Question Number 131732 by mnjuly1970 last updated on 07/Feb/21
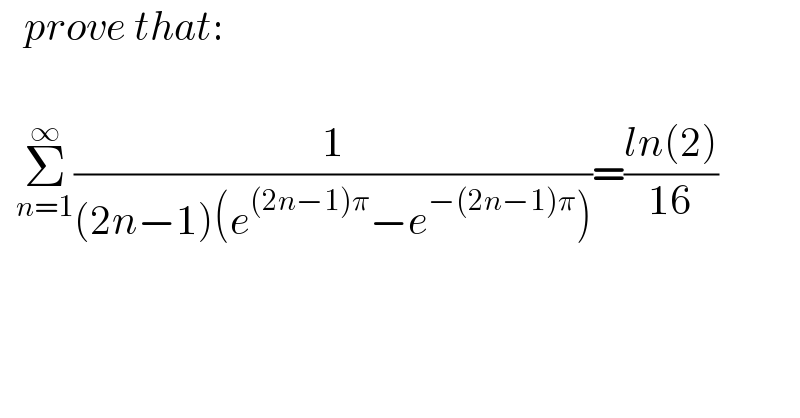
$$\:\:\:{prove}\:{that}: \\ $$$$\:\: \\ $$$$\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)\left({e}^{\left(\mathrm{2}{n}−\mathrm{1}\right)\pi} −{e}^{−\left(\mathrm{2}{n}−\mathrm{1}\right)\pi} \right)}=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{16}} \\ $$$$\: \\ $$
