Question Number 2112 by Yozzi last updated on 03/Nov/15
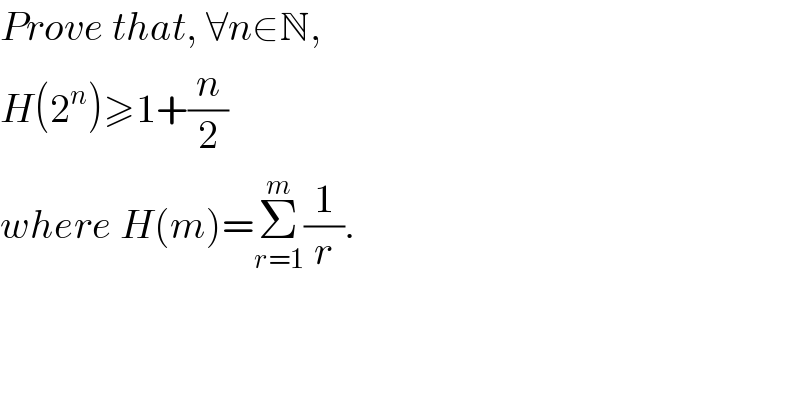
$${Prove}\:{that},\:\forall{n}\in\mathbb{N}, \\ $$$${H}\left(\mathrm{2}^{{n}} \right)\geqslant\mathrm{1}+\frac{{n}}{\mathrm{2}} \\ $$$${where}\:{H}\left({m}\right)=\underset{{r}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{\mathrm{1}}{{r}}. \\ $$
Commented by 123456 last updated on 03/Nov/15
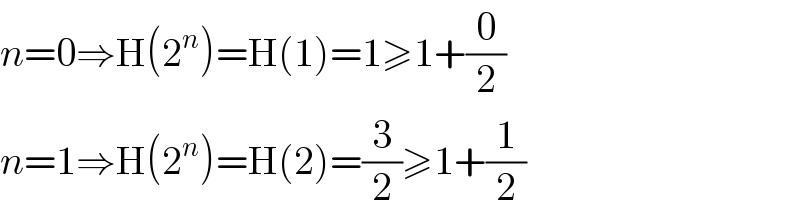
$${n}=\mathrm{0}\Rightarrow\mathrm{H}\left(\mathrm{2}^{{n}} \right)=\mathrm{H}\left(\mathrm{1}\right)=\mathrm{1}\geqslant\mathrm{1}+\frac{\mathrm{0}}{\mathrm{2}} \\ $$$${n}=\mathrm{1}\Rightarrow\mathrm{H}\left(\mathrm{2}^{{n}} \right)=\mathrm{H}\left(\mathrm{2}\right)=\frac{\mathrm{3}}{\mathrm{2}}\geqslant\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by 123456 last updated on 03/Nov/15

$$\mathrm{H}\left({m}\right)=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{{m}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:<\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{\mathrm{2}}\:\:{m}>\mathrm{2}\Rightarrow\frac{\mathrm{1}}{{m}}<\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:<\mathrm{1}+\frac{{m}−\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{H}\left({m}\right)>\mathrm{1}+\frac{\mathrm{1}}{{m}}+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{{m}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:>\mathrm{1}+\frac{{m}−\mathrm{1}}{{m}} \\ $$$$\mathrm{1}+\frac{{m}−\mathrm{1}}{{m}}<\mathrm{H}\left({m}\right)<\mathrm{1}+\frac{{m}−\mathrm{1}}{\mathrm{2}} \\ $$$$−−−−−−− \\ $$$$\mathrm{continue} \\ $$
Answered by prakash jain last updated on 04/Nov/15
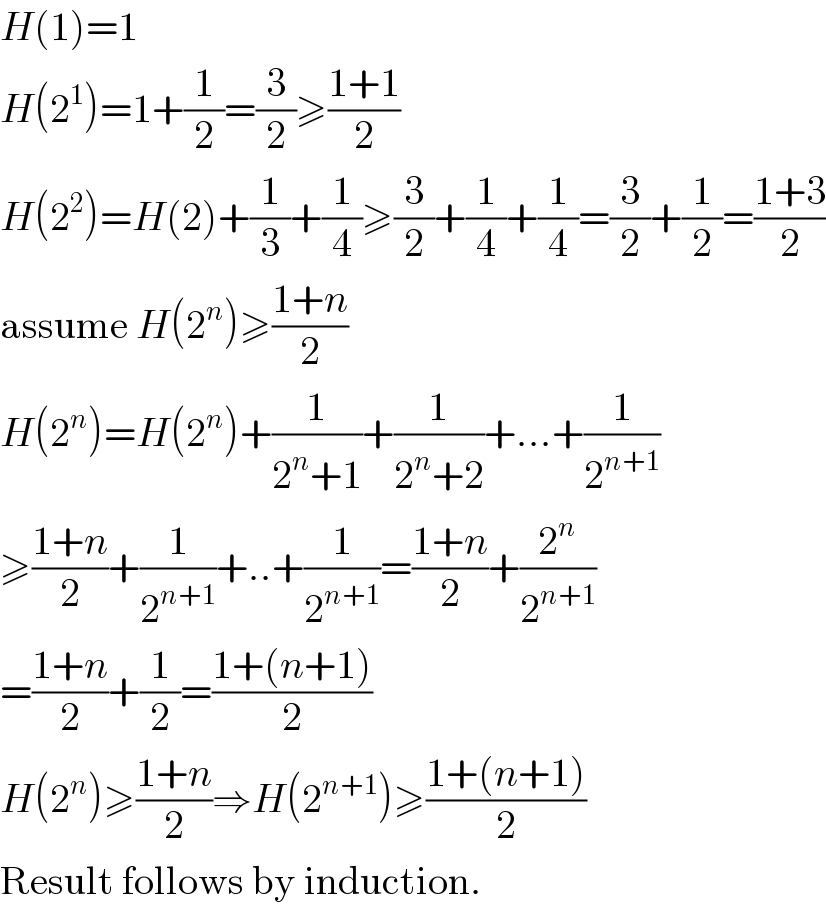
$${H}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$${H}\left(\mathrm{2}^{\mathrm{1}} \right)=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}}\geqslant\frac{\mathrm{1}+\mathrm{1}}{\mathrm{2}} \\ $$$${H}\left(\mathrm{2}^{\mathrm{2}} \right)={H}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}\geqslant\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}+\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{assume}\:{H}\left(\mathrm{2}^{{n}} \right)\geqslant\frac{\mathrm{1}+{n}}{\mathrm{2}} \\ $$$${H}\left(\mathrm{2}^{{n}} \right)={H}\left(\mathrm{2}^{{n}} \right)+\frac{\mathrm{1}}{\mathrm{2}^{{n}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}^{{n}} +\mathrm{2}}+…+\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$$\geqslant\frac{\mathrm{1}+{n}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }+..+\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }=\frac{\mathrm{1}+{n}}{\mathrm{2}}+\frac{\mathrm{2}^{{n}} }{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$$=\frac{\mathrm{1}+{n}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}+\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$${H}\left(\mathrm{2}^{{n}} \right)\geqslant\frac{\mathrm{1}+{n}}{\mathrm{2}}\Rightarrow{H}\left(\mathrm{2}^{{n}+\mathrm{1}} \right)\geqslant\frac{\mathrm{1}+\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{Result}\:\mathrm{follows}\:\mathrm{by}\:\mathrm{induction}. \\ $$
