Menu Close

Prove-that-n-N-k-1-n-1-sin-kpi-2n-k-1-n-1-cos-kpi-2n-

Tinku Tara 0 Comments
Pin




Question Number 142698 by Willson last updated on 04/Jun/21
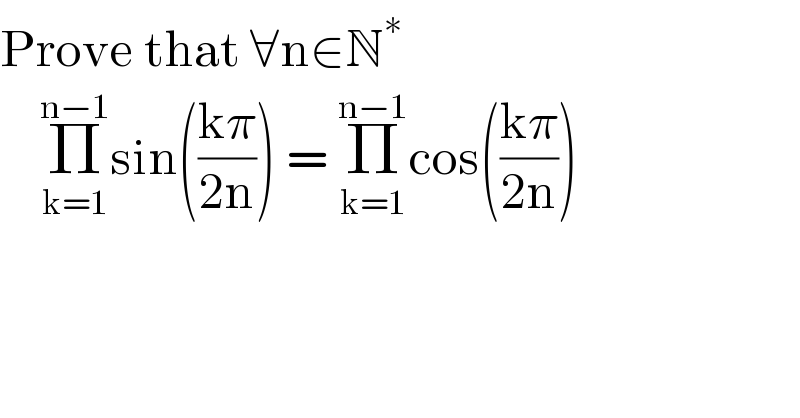
Prove that ∀n∈N^∗ Π_(k=1) ^(n−1) sin(((kπ)/(2n))) = Π_(k=1) ^(n−1) cos(((kπ)/(2n)))
$$\mathrm{Prove}\:\mathrm{that}\:\forall\mathrm{n}\in\mathbb{N}^{\ast} \\ $$$$\:\:\:\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\prod}}\mathrm{sin}\left(\frac{\mathrm{k}\pi}{\mathrm{2n}}\right)\:=\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\prod}}\mathrm{cos}\left(\frac{\mathrm{k}\pi}{\mathrm{2n}}\right) \\ $$
Answered by Ar Brandon last updated on 04/Jun/21
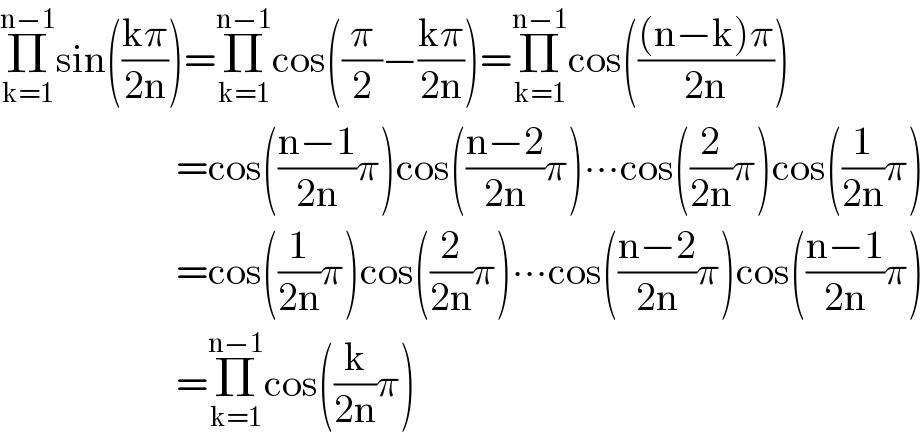
Π_(k=1) ^(n−1) sin(((kπ)/(2n)))=Π_(k=1) ^(n−1) cos((π/2)−((kπ)/(2n)))=Π_(k=1) ^(n−1) cos((((n−k)π)/(2n))) =cos(((n−1)/(2n))π)cos(((n−2)/(2n))π)∙∙∙cos((2/(2n))π)cos((1/(2n))π) =cos((1/(2n))π)cos((2/(2n))π)∙∙∙cos(((n−2)/(2n))π)cos(((n−1)/(2n))π) =Π_(k=1) ^(n−1) cos((k/(2n))π)
$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\prod}}\mathrm{sin}\left(\frac{\mathrm{k}\pi}{\mathrm{2n}}\right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\prod}}\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{k}\pi}{\mathrm{2n}}\right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\prod}}\mathrm{cos}\left(\frac{\left(\mathrm{n}−\mathrm{k}\right)\pi}{\mathrm{2n}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{cos}\left(\frac{\mathrm{n}−\mathrm{1}}{\mathrm{2n}}\pi\right)\mathrm{cos}\left(\frac{\mathrm{n}−\mathrm{2}}{\mathrm{2n}}\pi\right)\centerdot\centerdot\centerdot\mathrm{cos}\left(\frac{\mathrm{2}}{\mathrm{2n}}\pi\right)\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2n}}\pi\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2n}}\pi\right)\mathrm{cos}\left(\frac{\mathrm{2}}{\mathrm{2n}}\pi\right)\centerdot\centerdot\centerdot\mathrm{cos}\left(\frac{\mathrm{n}−\mathrm{2}}{\mathrm{2n}}\pi\right)\mathrm{cos}\left(\frac{\mathrm{n}−\mathrm{1}}{\mathrm{2n}}\pi\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\prod}}\mathrm{cos}\left(\frac{\mathrm{k}}{\mathrm{2n}}\pi\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *