Question Number 10670 by FilupS last updated on 22/Feb/17
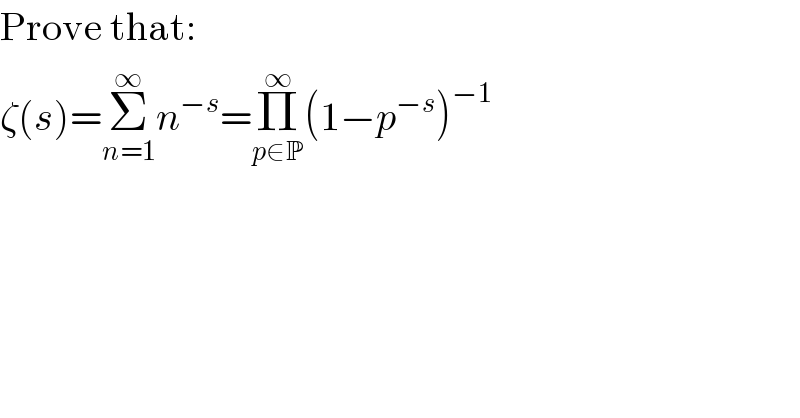
$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\zeta\left({s}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}^{−{s}} =\underset{{p}\in\mathbb{P}} {\overset{\infty} {\prod}}\left(\mathrm{1}−{p}^{−{s}} \right)^{−\mathrm{1}} \\ $$
