Menu Close

Prove-that-s-prime-1-1-p-s-

Tinku Tara 0 Comments
Pin




Question Number 142875 by Snail last updated on 06/Jun/21
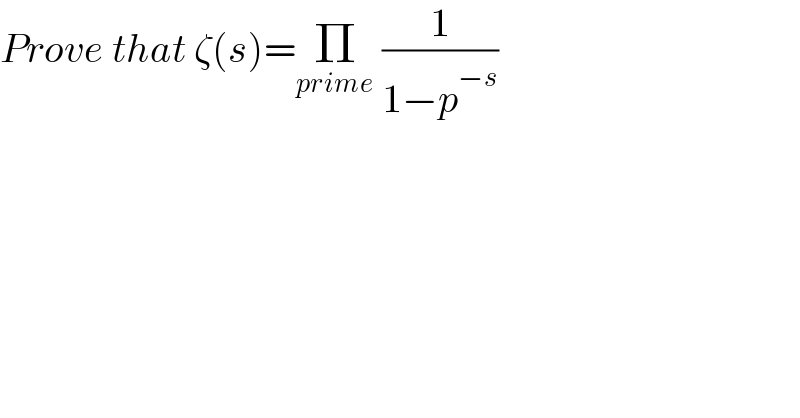
Prove that ζ(s)=Π_(prime) (1/(1−p^(−s) ))
$${Prove}\:{that}\:\zeta\left({s}\right)=\underset{{prime}} {\prod}\:\frac{\mathrm{1}}{\mathrm{1}−{p}^{−{s}} } \\ $$
Answered by Dwaipayan Shikari last updated on 06/Jun/21
ζ(s)=1+(1/2^s )+(1/3^s )+(1/4^s )+... ((ζ(s))/2^s )=(1/2^s )+(1/4^s )+(1/6^s )+... (Multiples of 2) ζ(s)(1−(1/2^s ))=1+(1/3^s )+(1/5^s )+(1/7^s )+... (Subtract) ζ(s)(1−(1/2^s ))(1/3^s )=(1/3^s )+(1/9^s )+(1/(15^s ))+(1/(21^s ))+...( all multiples of 3) ζ(s)(1−(1/2^s ))−ζ(s)(1−(1/2^s ))(1/3^s )=(1/1)+(1/5^s )+(1/7^s )+.. ζ(s)(1−(1/2^s ))(1−(1/3^s ))=1+(1/5^s )+(1/7^s )+.. Since each numbers(≠1) are bulid from primes , we can keep going like this ζ(s)(1−(1/2^s ))(1−(1/3^s ))(1−(1/5^s ))..=1 ζ(s)=Π_p ^∞ (1/(1−(1/p^s )))
$$\zeta\left({s}\right)=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{{s}} }+\frac{\mathrm{1}}{\mathrm{3}^{{s}} }+\frac{\mathrm{1}}{\mathrm{4}^{{s}} }+… \\ $$$$\frac{\zeta\left({s}\right)}{\mathrm{2}^{{s}} }=\frac{\mathrm{1}}{\mathrm{2}^{{s}} }+\frac{\mathrm{1}}{\mathrm{4}^{{s}} }+\frac{\mathrm{1}}{\mathrm{6}^{{s}} }+…\:\:\:\:\:\:\:\:\:\left({Multiples}\:{of}\:\mathrm{2}\right) \\ $$$$\zeta\left({s}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{s}} }\right)=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{{s}} }+\frac{\mathrm{1}}{\mathrm{5}^{{s}} }+\frac{\mathrm{1}}{\mathrm{7}^{{s}} }+…\:\:\left({Subtract}\right) \\ $$$$\zeta\left({s}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{s}} }\right)\frac{\mathrm{1}}{\mathrm{3}^{{s}} }=\frac{\mathrm{1}}{\mathrm{3}^{{s}} }+\frac{\mathrm{1}}{\mathrm{9}^{{s}} }+\frac{\mathrm{1}}{\mathrm{15}^{{s}} }+\frac{\mathrm{1}}{\mathrm{21}^{{s}} }+…\left(\:{all}\:{multiples}\:{of}\:\mathrm{3}\right) \\ $$$$\zeta\left({s}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{s}} }\right)−\zeta\left({s}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{s}} }\right)\frac{\mathrm{1}}{\mathrm{3}^{{s}} }=\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{5}^{{s}} }+\frac{\mathrm{1}}{\mathrm{7}^{{s}} }+.. \\ $$$$\zeta\left({s}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{s}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{{s}} }\right)=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{5}^{{s}} }+\frac{\mathrm{1}}{\mathrm{7}^{{s}} }+..\:\: \\ $$$${Since}\:{each}\:{numbers}\left(\neq\mathrm{1}\right)\:{are}\:{bulid}\:{from}\:{primes}\:, \\ $$$${we}\:{can}\:{keep}\:{going}\:{like}\:{this} \\ $$$$ \\ $$$$\zeta\left({s}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{s}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{{s}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}^{{s}} }\right)..=\mathrm{1} \\ $$$$\zeta\left({s}\right)=\underset{{p}} {\overset{\infty} {\prod}}\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{{p}^{{s}} }} \\ $$
Commented by Snail last updated on 06/Jun/21
Thanks
$${Thanks} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *