Menu Close

Prove-that-S-x-y-z-R-3-x-2-y-2-z-2-is-a-surface-and-find-out-if-possible-the-tangent-plan-in-O-0-0-0-

Tinku Tara 0 Comments
Pin




Question Number 74301 by ~blr237~ last updated on 21/Nov/19
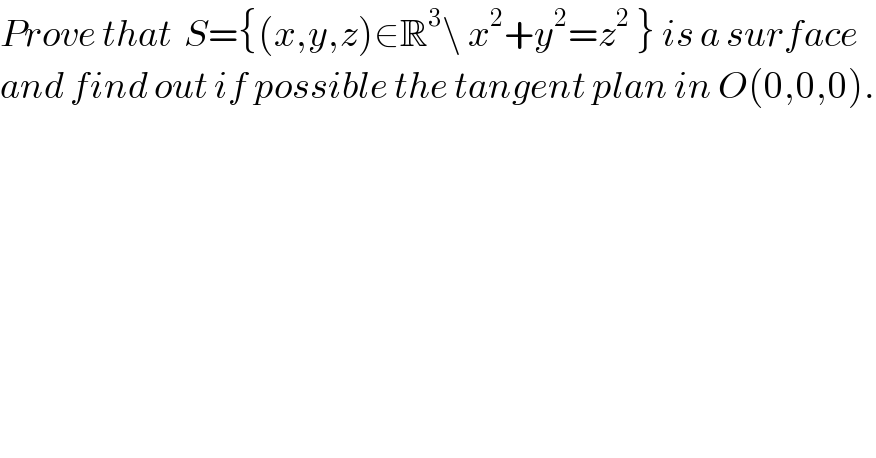
Prove that S={(x,y,z)∈R^3 \ x^2 +y^2 =z^2 } is a surface and find out if possible the tangent plan in O(0,0,0).
$${Prove}\:{that}\:\:{S}=\left\{\left({x},{y},{z}\right)\in\mathbb{R}^{\mathrm{3}} \backslash\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={z}^{\mathrm{2}} \:\right\}\:{is}\:{a}\:{surface}\: \\ $$$${and}\:{find}\:{out}\:{if}\:{possible}\:{the}\:{tangent}\:{plan}\:{in}\:{O}\left(\mathrm{0},\mathrm{0},\mathrm{0}\right). \\ $$
Answered by mind is power last updated on 21/Nov/19
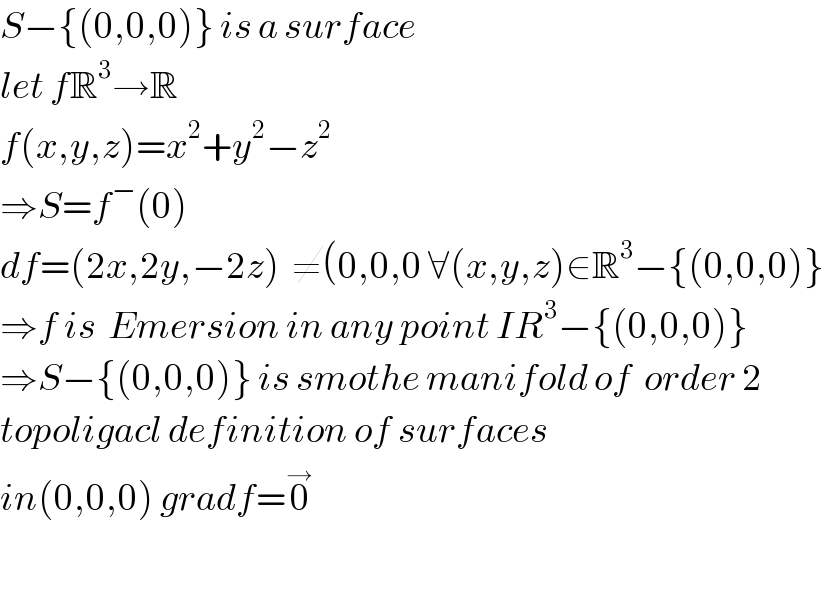
S−{(0,0,0)} is a surface let fR^3 →R f(x,y,z)=x^2 +y^2 −z^2 ⇒S=f^− (0) df=(2x,2y,−2z) ≠(0,0,0 ∀(x,y,z)∈R^3 −{(0,0,0)} ⇒f is Emersion in any point IR^3 −{(0,0,0)} ⇒S−{(0,0,0)} is smothe manifold of order 2 topoligacl definition of surfaces in(0,0,0) gradf=0^→
$${S}−\left\{\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)\right\}\:{is}\:{a}\:{surface}\: \\ $$$${let}\:{f}\mathbb{R}^{\mathrm{3}} \rightarrow\mathbb{R} \\ $$$${f}\left({x},{y},{z}\right)={x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{z}^{\mathrm{2}} \\ $$$$\Rightarrow{S}={f}^{−} \left(\mathrm{0}\right) \\ $$$${df}=\left(\mathrm{2}{x},\mathrm{2}{y},−\mathrm{2}{z}\right)\:\:\neq\left(\mathrm{0},\mathrm{0},\mathrm{0}\:\forall\left({x},{y},{z}\right)\in\mathbb{R}^{\mathrm{3}} −\left\{\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)\right\}\right. \\ $$$$\Rightarrow{f}\:{is}\:\:{Emersion}\:{in}\:{any}\:{point}\:{IR}^{\mathrm{3}} −\left\{\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)\right\} \\ $$$$\Rightarrow{S}−\left\{\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)\right\}\:{is}\:{smothe}\:{manifold}\:{of}\:\:{order}\:\mathrm{2}\: \\ $$$${topoligacl}\:{definition}\:{of}\:{surfaces} \\ $$$${in}\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)\:{gradf}=\overset{\rightarrow} {\mathrm{0}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *