Question Number 12378 by tawa last updated on 20/Apr/17
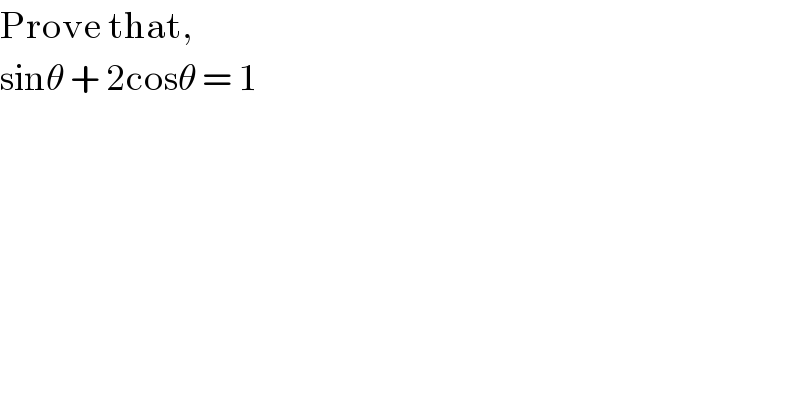
$$\mathrm{Prove}\:\mathrm{that}, \\ $$$$\mathrm{sin}\theta\:+\:\mathrm{2cos}\theta\:=\:\mathrm{1} \\ $$
Commented by mrW1 last updated on 21/Apr/17
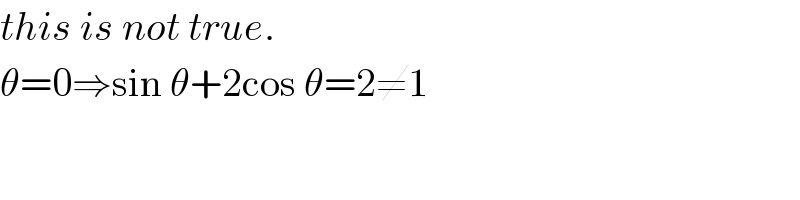
$${this}\:{is}\:{not}\:{true}.\: \\ $$$$\theta=\mathrm{0}\Rightarrow\mathrm{sin}\:\theta+\mathrm{2cos}\:\theta=\mathrm{2}\neq\mathrm{1} \\ $$
Commented by tawa last updated on 21/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by mrW1 last updated on 23/Apr/17
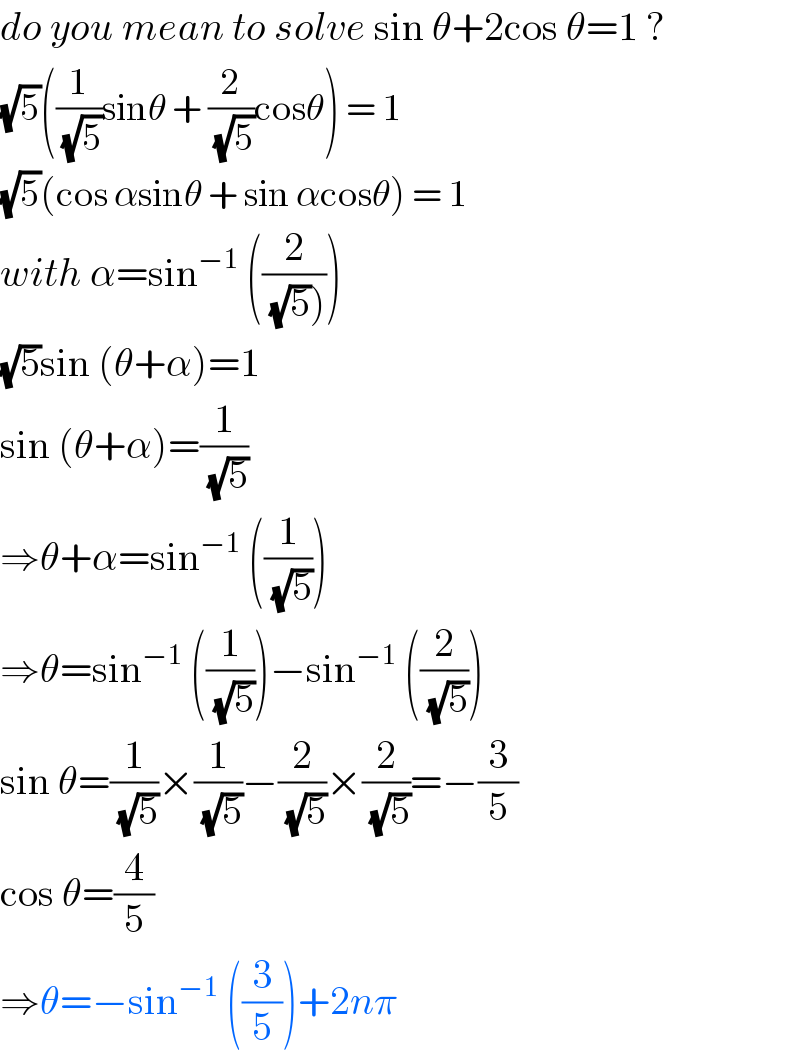
$${do}\:{you}\:{mean}\:{to}\:{solve}\:\mathrm{sin}\:\theta+\mathrm{2cos}\:\theta=\mathrm{1}\:? \\ $$$$\sqrt{\mathrm{5}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\mathrm{sin}\theta\:+\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\mathrm{cos}\theta\right)\:=\:\mathrm{1} \\ $$$$\sqrt{\mathrm{5}}\left(\mathrm{cos}\:\alpha\mathrm{sin}\theta\:+\:\mathrm{sin}\:\alpha\mathrm{cos}\theta\right)\:=\:\mathrm{1} \\ $$$${with}\:\alpha=\mathrm{sin}^{−\mathrm{1}} \:\left(\frac{\mathrm{2}}{\left.\:\sqrt{\mathrm{5}}\right)}\right) \\ $$$$\sqrt{\mathrm{5}}\mathrm{sin}\:\left(\theta+\alpha\right)=\mathrm{1} \\ $$$$\mathrm{sin}\:\left(\theta+\alpha\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow\theta+\alpha=\mathrm{sin}^{−\mathrm{1}} \:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right) \\ $$$$\Rightarrow\theta=\mathrm{sin}^{−\mathrm{1}} \:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)−\mathrm{sin}^{−\mathrm{1}} \:\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\right) \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}=−\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\mathrm{cos}\:\theta=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\Rightarrow\theta=−\mathrm{sin}^{−\mathrm{1}} \:\left(\frac{\mathrm{3}}{\mathrm{5}}\right)+\mathrm{2}{n}\pi \\ $$
