Question Number 131879 by Study last updated on 09/Feb/21
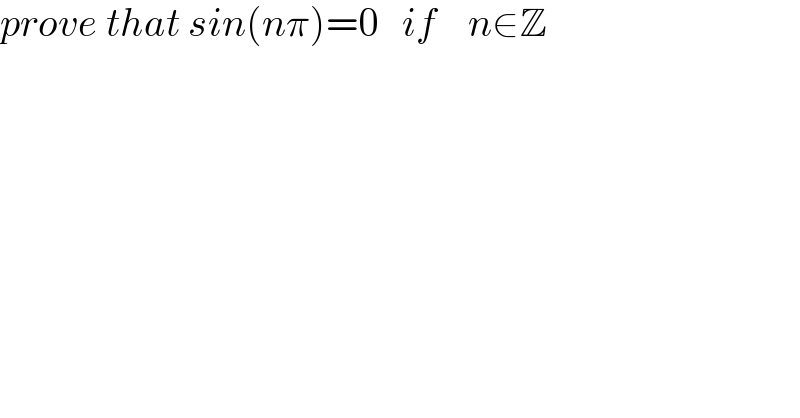
$${prove}\:{that}\:{sin}\left({n}\pi\right)=\mathrm{0}\:\:\:{if}\:\:\:\:{n}\in\mathbb{Z} \\ $$
Answered by physicstutes last updated on 10/Feb/21
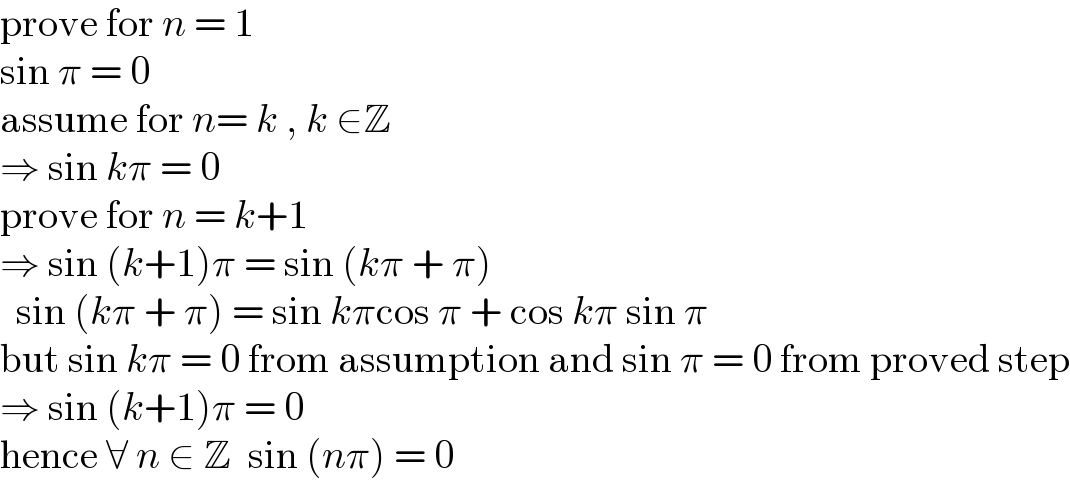
$$\mathrm{prove}\:\mathrm{for}\:{n}\:=\:\mathrm{1} \\ $$$$\mathrm{sin}\:\pi\:=\:\mathrm{0} \\ $$$$\mathrm{assume}\:\mathrm{for}\:{n}=\:{k}\:,\:{k}\:\in\mathbb{Z} \\ $$$$\Rightarrow\:\mathrm{sin}\:{k}\pi\:=\:\mathrm{0} \\ $$$$\mathrm{prove}\:\mathrm{for}\:{n}\:=\:{k}+\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{sin}\:\left({k}+\mathrm{1}\right)\pi\:=\:\mathrm{sin}\:\left({k}\pi\:+\:\pi\right) \\ $$$$\:\:\mathrm{sin}\:\left({k}\pi\:+\:\pi\right)\:=\:\mathrm{sin}\:{k}\pi\mathrm{cos}\:\pi\:+\:\mathrm{cos}\:{k}\pi\:\mathrm{sin}\:\pi \\ $$$$\mathrm{but}\:\mathrm{sin}\:{k}\pi\:=\:\mathrm{0}\:\mathrm{from}\:\mathrm{assumption}\:\mathrm{and}\:\mathrm{sin}\:\pi\:=\:\mathrm{0}\:\mathrm{from}\:\mathrm{proved}\:\mathrm{step} \\ $$$$\Rightarrow\:\mathrm{sin}\:\left({k}+\mathrm{1}\right)\pi\:=\:\mathrm{0}\: \\ $$$$\mathrm{hence}\:\forall\:{n}\:\in\:\mathbb{Z}\:\:\mathrm{sin}\:\left({n}\pi\right)\:=\:\mathrm{0}\: \\ $$
