Question Number 10542 by FilupS last updated on 17/Feb/17
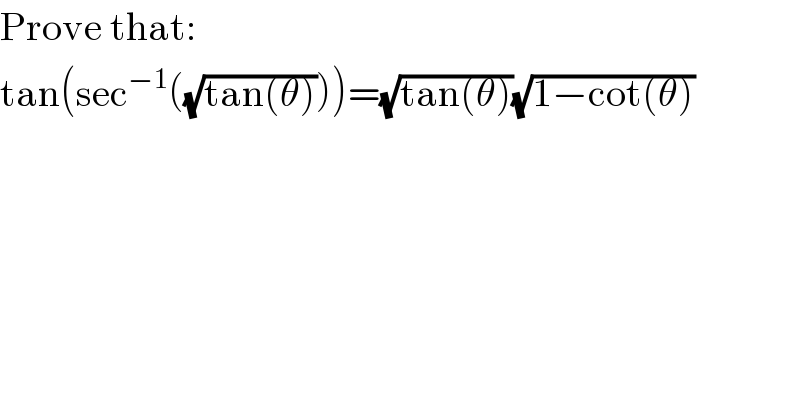
$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\mathrm{tan}\left(\mathrm{sec}^{−\mathrm{1}} \left(\sqrt{\mathrm{tan}\left(\theta\right)}\right)\right)=\sqrt{\mathrm{tan}\left(\theta\right)}\sqrt{\mathrm{1}−\mathrm{cot}\left(\theta\right)} \\ $$
Answered by mrW1 last updated on 17/Feb/17
![let α=sec^(−1) ((√(tan (θ)))) ⇒sec α=(√(tan (θ))) ⇒sec^2 α=tan (θ) tan(sec^(−1) ((√(tan(θ)))))=tan α=(√(sec^2 α−1))=(√(tan (θ)−1))=(√(tan (θ)[1−(1/(tan (θ)))]))=(√(tan (θ)))(√(1−cot (θ))) proven!](https://www.tinkutara.com/question/Q10548.png)
$${let}\:\alpha=\mathrm{sec}^{−\mathrm{1}} \left(\sqrt{\mathrm{tan}\:\left(\theta\right)}\right) \\ $$$$\Rightarrow\mathrm{sec}\:\alpha=\sqrt{\mathrm{tan}\:\left(\theta\right)} \\ $$$$\Rightarrow\mathrm{sec}^{\mathrm{2}} \:\alpha=\mathrm{tan}\:\left(\theta\right) \\ $$$$\mathrm{tan}\left(\mathrm{sec}^{−\mathrm{1}} \left(\sqrt{\mathrm{tan}\left(\theta\right)}\right)\right)=\mathrm{tan}\:\alpha=\sqrt{\mathrm{sec}^{\mathrm{2}} \:\alpha−\mathrm{1}}=\sqrt{\mathrm{t}{a}\mathrm{n}\:\left(\theta\right)−\mathrm{1}}=\sqrt{\mathrm{tan}\:\left(\theta\right)\left[\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\left(\theta\right)}\right]}=\sqrt{\mathrm{tan}\:\left(\theta\right)}\sqrt{\mathrm{1}−\mathrm{cot}\:\left(\theta\right)} \\ $$$${proven}! \\ $$
