Question Number 72693 by Rio Michael last updated on 31/Oct/19

$${prove}\:{that}\:{the}\:{arithmetic}\:{mean}\:{of}\:{a}\:{sequence} \\ $$$${is}\:{greater}\:{or}\:{equal}\:{to}\:{the}\:{geometric}\:{mean}. \\ $$$${that}\:\:{is}\:\: \\ $$$$\:\:\:\:\frac{{a}\:+\:{b}}{\mathrm{2}}\:\geqslant\:\sqrt{{ab}}\: \\ $$
Answered by MJS last updated on 31/Oct/19
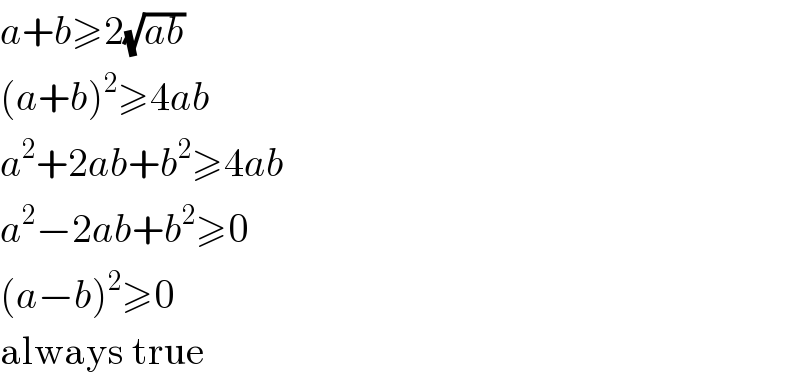
$${a}+{b}\geqslant\mathrm{2}\sqrt{{ab}} \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} \geqslant\mathrm{4}{ab} \\ $$$${a}^{\mathrm{2}} +\mathrm{2}{ab}+{b}^{\mathrm{2}} \geqslant\mathrm{4}{ab} \\ $$$${a}^{\mathrm{2}} −\mathrm{2}{ab}+{b}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\left({a}−{b}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\mathrm{always}\:\mathrm{true} \\ $$
Commented by Rio Michael last updated on 31/Oct/19

$${thank}\:{you}\:{sir} \\ $$
