Question Number 11834 by Mr Chheang Chantria last updated on 02/Apr/17
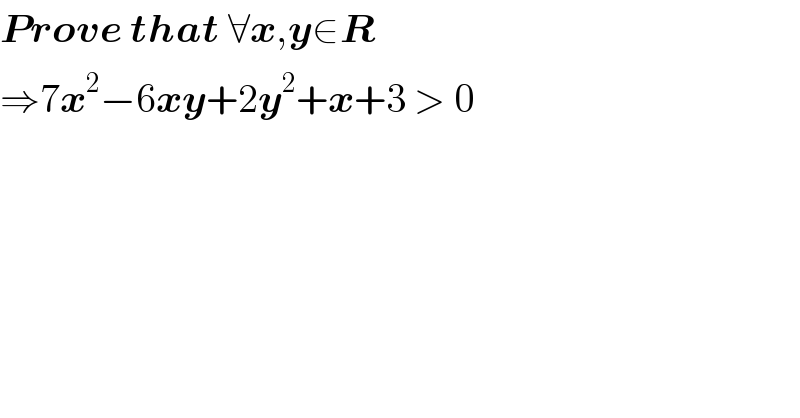
$$\boldsymbol{{Prove}}\:\boldsymbol{{that}}\:\forall\boldsymbol{{x}},\boldsymbol{{y}}\in\boldsymbol{{R}} \\ $$$$\Rightarrow\mathrm{7}\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{6}\boldsymbol{{xy}}+\mathrm{2}\boldsymbol{{y}}^{\mathrm{2}} +\boldsymbol{{x}}+\mathrm{3}\:>\:\mathrm{0} \\ $$
Answered by mrW1 last updated on 02/Apr/17
![7x^2 −6xy+2y^2 +x+3 =((3/( (√2)))x)^2 −2×(3/( (√2)))x×(√2)y+((√2)y)^2 +((1/2)x)^2 +2×(1/2)x+1+[7−((3/( (√2))))^2 −((1/2))^2 ]x^2 +(3−1) =((3/( (√2)))x−(√2)y)^2 +((1/2)x+1)^2 +((3/2)x)^2 +2 >2>0](https://www.tinkutara.com/question/Q11837.png)
$$\mathrm{7}\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{6}\boldsymbol{{xy}}+\mathrm{2}\boldsymbol{{y}}^{\mathrm{2}} +\boldsymbol{{x}}+\mathrm{3} \\ $$$$=\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}{x}\right)^{\mathrm{2}} −\mathrm{2}×\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}{x}×\sqrt{\mathrm{2}}{y}+\left(\sqrt{\mathrm{2}}{y}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}{x}\right)^{\mathrm{2}} +\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{1}+\left[\mathrm{7}−\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \right]{x}^{\mathrm{2}} +\left(\mathrm{3}−\mathrm{1}\right) \\ $$$$=\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}{x}−\sqrt{\mathrm{2}}{y}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{1}\right)^{\mathrm{2}} +\left(\frac{\mathrm{3}}{\mathrm{2}}{x}\right)^{\mathrm{2}} +\mathrm{2} \\ $$$$>\mathrm{2}>\mathrm{0} \\ $$
Commented by Mr Chheang Chantria last updated on 03/Apr/17
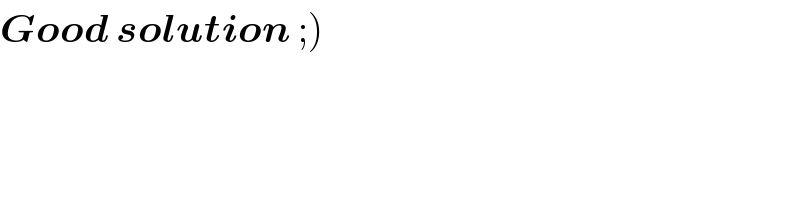
$$\left.\boldsymbol{{Good}}\:\boldsymbol{{solution}}\:;\right) \\ $$$$ \\ $$
Answered by ajfour last updated on 02/Apr/17
![6x^2 −6xy+2y^2 +x^2 +x+3 =2x^2 [3−((3y)/x)+((y/x))^2 ]+(x+(1/2))^2 −(1/4)+3 =2x^2 [((y/x)−(3/2))^2 −(9/4)+3 ]+(x+(1/2))^2 +((11)/4) =2x^2 [(((2y−3x)^2 )/(4x^2 ))+(3/4)]+(x+(1/2))^2 +((11)/4) =(((2y−3x)^2 )/2)+((3x^2 )/2)+(x+(1/2))^2 +((11)/4) >0](https://www.tinkutara.com/question/Q11842.png)
$$\mathrm{6}{x}^{\mathrm{2}} −\mathrm{6}{xy}+\mathrm{2}{y}^{\mathrm{2}} +{x}^{\mathrm{2}} +{x}+\mathrm{3} \\ $$$$=\mathrm{2}{x}^{\mathrm{2}} \left[\mathrm{3}−\frac{\mathrm{3}{y}}{{x}}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} \:\right]+\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{3} \\ $$$$=\mathrm{2}{x}^{\mathrm{2}} \left[\left(\frac{{y}}{{x}}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{4}}+\mathrm{3}\:\right]+\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{11}}{\mathrm{4}} \\ $$$$=\mathrm{2}{x}^{\mathrm{2}} \left[\frac{\left(\mathrm{2}{y}−\mathrm{3}{x}\right)^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{4}}\right]+\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{11}}{\mathrm{4}} \\ $$$$=\frac{\left(\mathrm{2}{y}−\mathrm{3}{x}\right)^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}+\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{11}}{\mathrm{4}}\:>\mathrm{0} \\ $$
Commented by Mr Chheang Chantria last updated on 03/Apr/17

$$\left.\boldsymbol{\mathrm{that}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{sweet}}\:;\right) \\ $$$$ \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 02/Apr/17
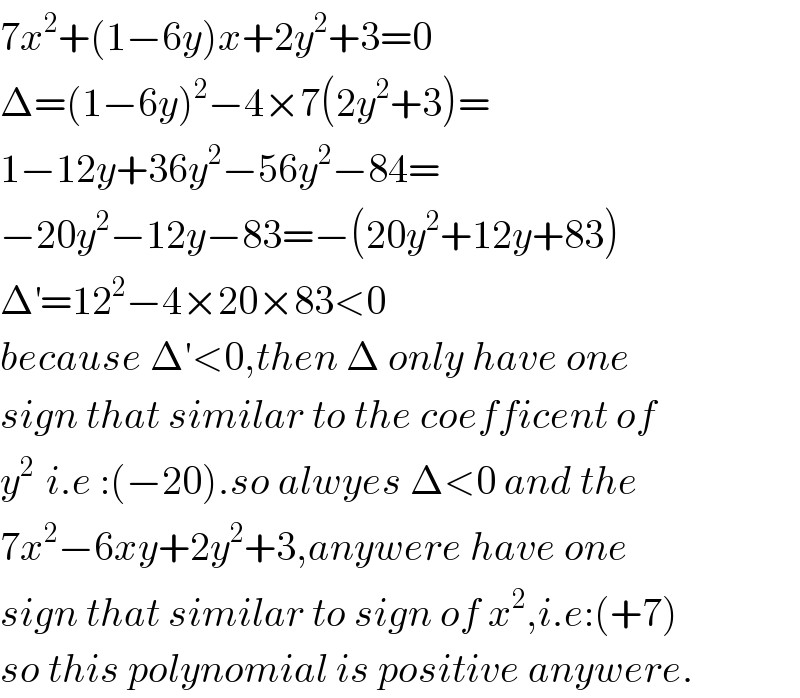
$$\mathrm{7}{x}^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{6}{y}\right){x}+\mathrm{2}{y}^{\mathrm{2}} +\mathrm{3}=\mathrm{0} \\ $$$$\Delta=\left(\mathrm{1}−\mathrm{6}{y}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{7}\left(\mathrm{2}{y}^{\mathrm{2}} +\mathrm{3}\right)= \\ $$$$\mathrm{1}−\mathrm{12}{y}+\mathrm{36}{y}^{\mathrm{2}} −\mathrm{56}{y}^{\mathrm{2}} −\mathrm{84}= \\ $$$$−\mathrm{20}{y}^{\mathrm{2}} −\mathrm{12}{y}−\mathrm{83}=−\left(\mathrm{20}{y}^{\mathrm{2}} +\mathrm{12}{y}+\mathrm{83}\right) \\ $$$$\Delta^{'} =\mathrm{12}^{\mathrm{2}} −\mathrm{4}×\mathrm{20}×\mathrm{83}<\mathrm{0} \\ $$$${because}\:\Delta'<\mathrm{0},{then}\:\Delta\:{only}\:{have}\:{one} \\ $$$${sign}\:{that}\:{similar}\:{to}\:{the}\:{coefficent}\:{of} \\ $$$${y}^{\mathrm{2}\:} \:{i}.{e}\::\left(−\mathrm{20}\right).{so}\:{alwyes}\:\Delta<\mathrm{0}\:{and}\:{the} \\ $$$$\mathrm{7}{x}^{\mathrm{2}} −\mathrm{6}{xy}+\mathrm{2}{y}^{\mathrm{2}} +\mathrm{3},{anywere}\:{have}\:{one} \\ $$$${sign}\:{that}\:{similar}\:{to}\:{sign}\:{of}\:{x}^{\mathrm{2}} ,{i}.{e}:\left(+\mathrm{7}\right) \\ $$$${so}\:{this}\:{polynomial}\:{is}\:{positive}\:{anywere}. \\ $$
Commented by mrW1 last updated on 02/Apr/17
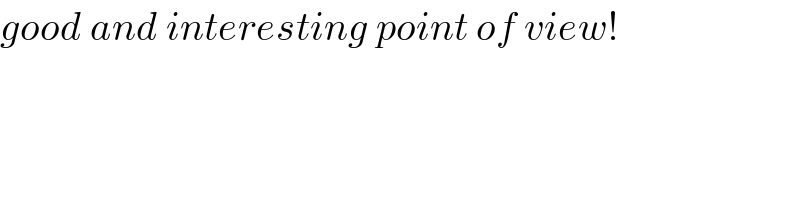
$${good}\:{and}\:{interesting}\:{point}\:{of}\:{view}! \\ $$
Commented by Mr Chheang Chantria last updated on 03/Apr/17
$$\boldsymbol{{nice}}\:\boldsymbol{{solution}}\:\boldsymbol{{and}}\:\boldsymbol{{nice}}\:\boldsymbol{{explain}} \\ $$$$\left.\boldsymbol{{Thanks}}\:\boldsymbol{{you}}\:;\right) \\ $$
