Question Number 5874 by sanusihammed last updated on 02/Jun/16
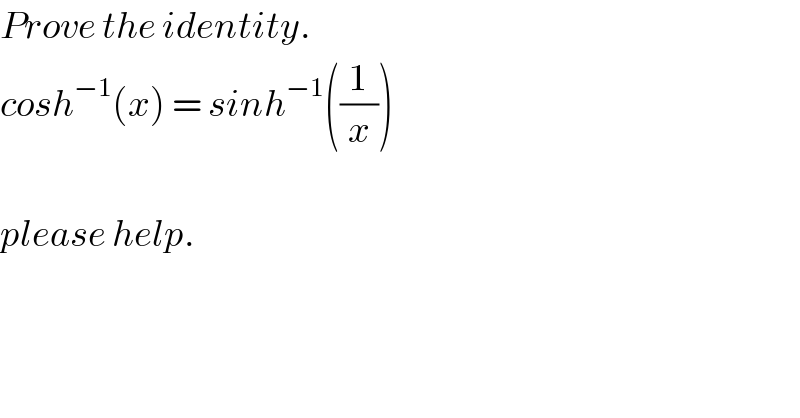
$${Prove}\:{the}\:{identity}.\: \\ $$$${cosh}^{−\mathrm{1}} \left({x}\right)\:=\:{sinh}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{x}}\right) \\ $$$$ \\ $$$${please}\:{help}. \\ $$
Answered by Yozzii last updated on 02/Jun/16
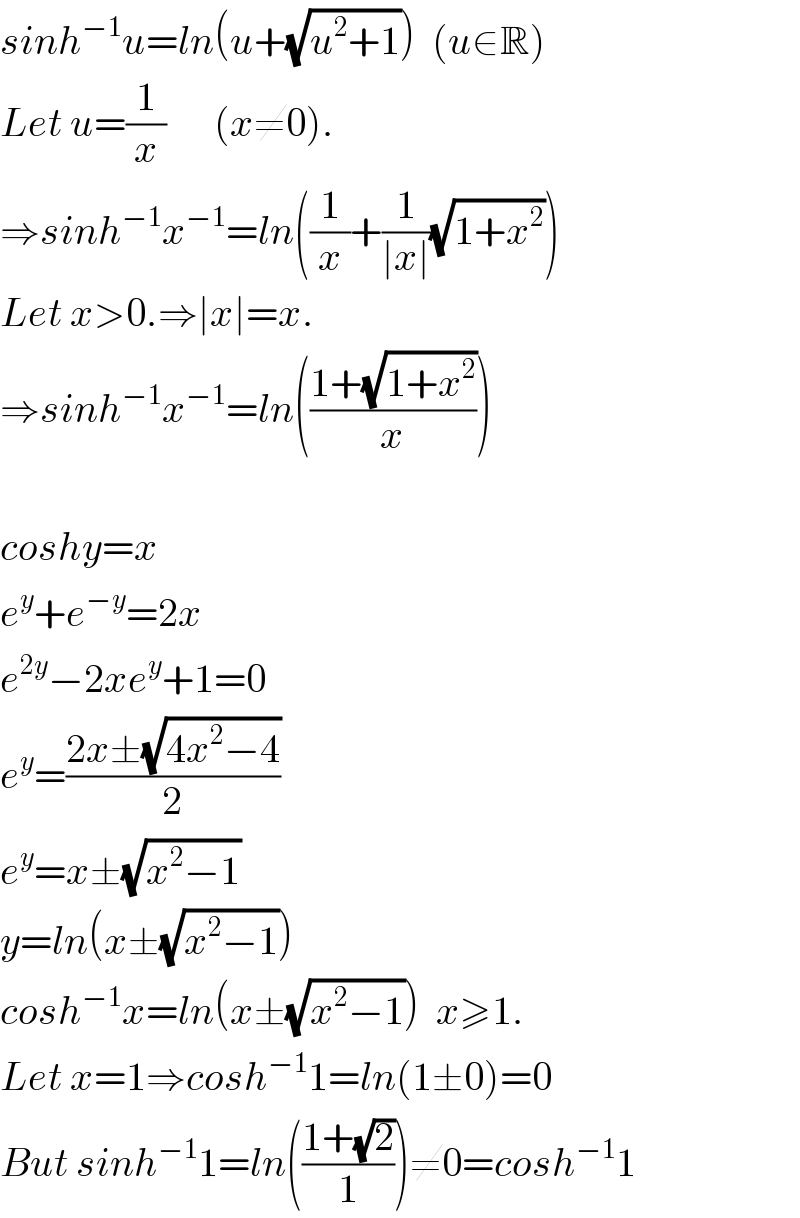
$${sinh}^{−\mathrm{1}} {u}={ln}\left({u}+\sqrt{{u}^{\mathrm{2}} +\mathrm{1}}\right)\:\:\left({u}\in\mathbb{R}\right) \\ $$$${Let}\:{u}=\frac{\mathrm{1}}{{x}}\:\:\:\:\:\:\left({x}\neq\mathrm{0}\right). \\ $$$$\Rightarrow{sinh}^{−\mathrm{1}} {x}^{−\mathrm{1}} ={ln}\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mid{x}\mid}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right) \\ $$$${Let}\:{x}>\mathrm{0}.\Rightarrow\mid{x}\mid={x}. \\ $$$$\Rightarrow{sinh}^{−\mathrm{1}} {x}^{−\mathrm{1}} ={ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}}\right) \\ $$$$ \\ $$$${coshy}={x} \\ $$$${e}^{{y}} +{e}^{−{y}} =\mathrm{2}{x} \\ $$$${e}^{\mathrm{2}{y}} −\mathrm{2}{xe}^{{y}} +\mathrm{1}=\mathrm{0} \\ $$$${e}^{{y}} =\frac{\mathrm{2}{x}\pm\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}} \\ $$$${e}^{{y}} ={x}\pm\sqrt{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$${y}={ln}\left({x}\pm\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$${cosh}^{−\mathrm{1}} {x}={ln}\left({x}\pm\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)\:\:{x}\geqslant\mathrm{1}. \\ $$$${Let}\:{x}=\mathrm{1}\Rightarrow{cosh}^{−\mathrm{1}} \mathrm{1}={ln}\left(\mathrm{1}\pm\mathrm{0}\right)=\mathrm{0} \\ $$$${But}\:{sinh}^{−\mathrm{1}} \mathrm{1}={ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{1}}\right)\neq\mathrm{0}={cosh}^{−\mathrm{1}} \mathrm{1} \\ $$
