Question Number 70601 by oyemi kemewari last updated on 06/Oct/19
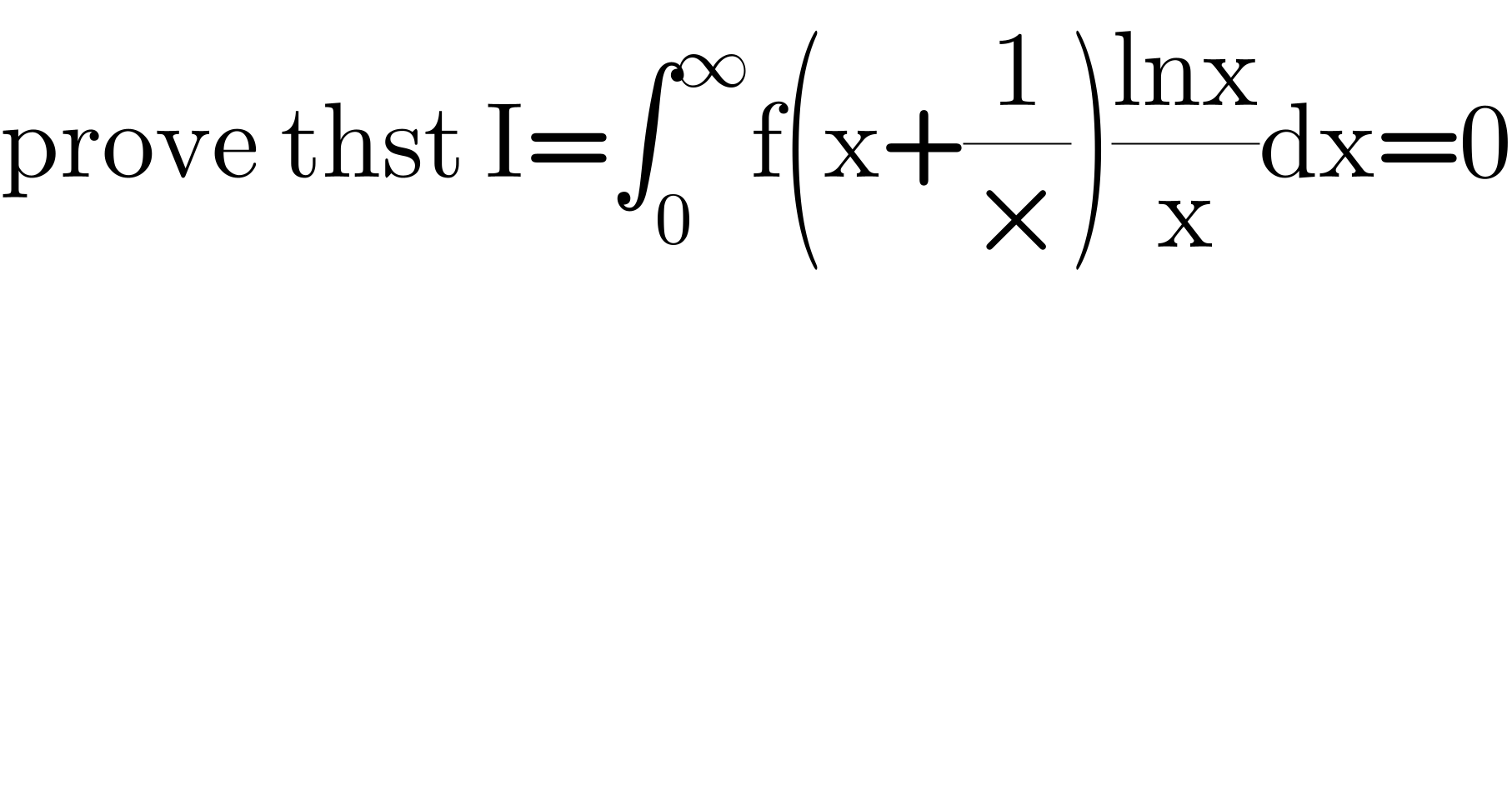
$$\mathrm{prove}\:\mathrm{thst}\:\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \mathrm{f}\left(\mathrm{x}+\frac{\mathrm{1}}{×}\right)\frac{\mathrm{lnx}}{\mathrm{x}}\mathrm{dx}=\mathrm{0} \\ $$
Answered by mind is power last updated on 06/Oct/19
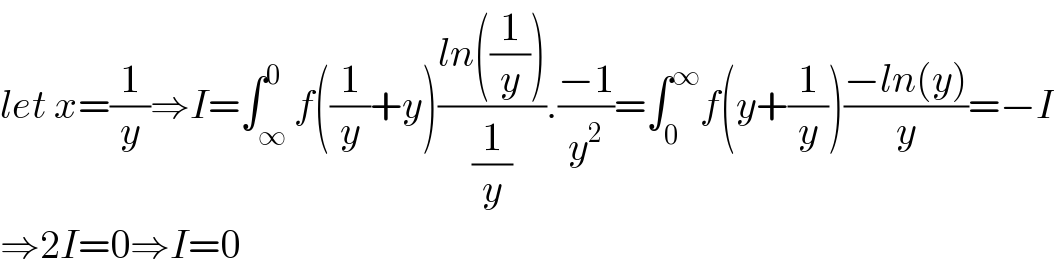
$${let}\:{x}=\frac{\mathrm{1}}{{y}}\Rightarrow{I}=\int_{\infty} ^{\mathrm{0}} {f}\left(\frac{\mathrm{1}}{{y}}+{y}\right)\frac{{ln}\left(\frac{\mathrm{1}}{{y}}\right)}{\frac{\mathrm{1}}{{y}}}.\frac{−\mathrm{1}}{{y}^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\infty} {f}\left({y}+\frac{\mathrm{1}}{{y}}\right)\frac{−{ln}\left({y}\right)}{{y}}=−{I} \\ $$$$\Rightarrow\mathrm{2}{I}=\mathrm{0}\Rightarrow{I}=\mathrm{0} \\ $$
Commented by oyemi kemewari last updated on 07/Oct/19
thank you sir
