Menu Close

Q-1-1-cos-2-2A-2-cos-4-A-sin-4-A-2-sin-2-A-sin-2-120-0-A-sin-2-120-0-A-3-2-

Tinku Tara 0 Comments
Pin




Question Number 8401 by rhm last updated on 10/Oct/16
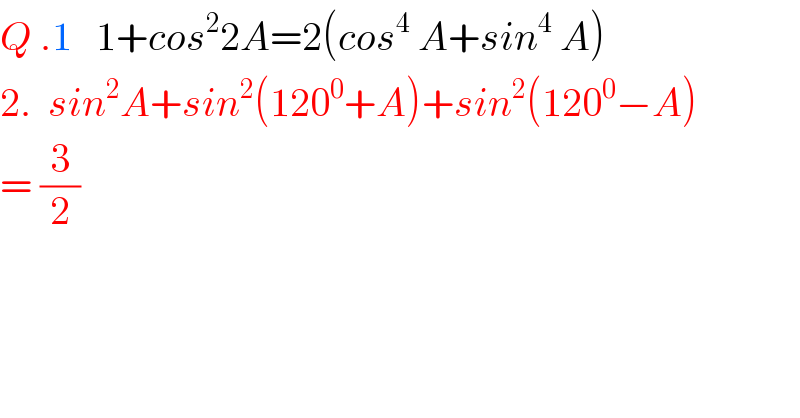
Q .1 1+cos^2 2A=2(cos^4 A+sin^4 A) 2. sin^2 A+sin^2 (120^0 +A)+sin^2 (120^0 −A) = (3/2)
$${Q}\:.\mathrm{1}\:\:\:\mathrm{1}+{cos}^{\mathrm{2}} \mathrm{2}{A}=\mathrm{2}\left({cos}^{\mathrm{4}} \:{A}+{sin}^{\mathrm{4}} \:{A}\right) \\ $$$$\mathrm{2}.\:\:{sin}^{\mathrm{2}} {A}+{sin}^{\mathrm{2}} \left(\mathrm{120}^{\mathrm{0}} +{A}\right)+{sin}^{\mathrm{2}} \left(\mathrm{120}^{\mathrm{0}} −{A}\right) \\ $$$$=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$ \\ $$
Answered by ridwan balatif last updated on 10/Oct/16
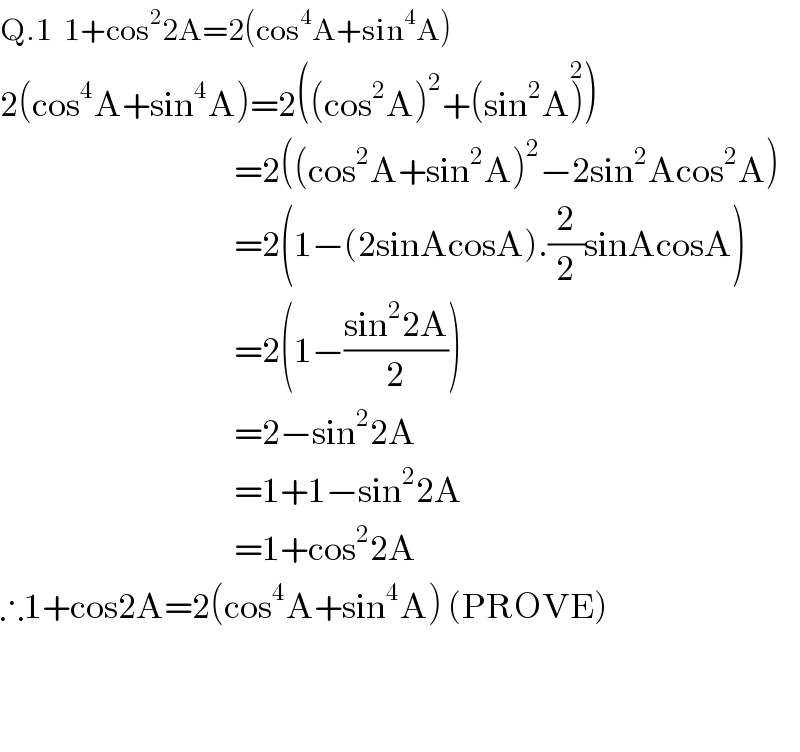
Q.1 1+cos^2 2A=2(cos^4 A+sin^4 A) 2(cos^4 A+sin^4 A)=2((cos^2 A)^2 +(sin^2 A)^2 ) =2((cos^2 A+sin^2 A)^2 −2sin^2 Acos^2 A) =2(1−(2sinAcosA).(2/2)sinAcosA) =2(1−((sin^2 2A)/2)) =2−sin^2 2A =1+1−sin^2 2A =1+cos^2 2A ∴1+cos2A=2(cos^4 A+sin^4 A) (PROVE)
$$\mathrm{Q}.\mathrm{1}\:\:\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{2A}=\mathrm{2}\left(\mathrm{cos}^{\mathrm{4}} \mathrm{A}+\mathrm{sin}^{\mathrm{4}} \mathrm{A}\right) \\ $$$$\mathrm{2}\left(\mathrm{cos}^{\mathrm{4}} \mathrm{A}+\mathrm{sin}^{\mathrm{4}} \mathrm{A}\right)=\mathrm{2}\left(\left(\mathrm{cos}^{\mathrm{2}} \mathrm{A}\right)^{\mathrm{2}} +\left(\mathrm{sin}^{\mathrm{2}} \mathrm{A}\overset{\mathrm{2}} {\right)}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left(\left(\mathrm{cos}^{\mathrm{2}} \mathrm{A}+\mathrm{sin}^{\mathrm{2}} \mathrm{A}\right)^{\mathrm{2}} −\mathrm{2sin}^{\mathrm{2}} \mathrm{Acos}^{\mathrm{2}} \mathrm{A}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left(\mathrm{1}−\left(\mathrm{2sinAcosA}\right).\frac{\mathrm{2}}{\mathrm{2}}\mathrm{sinAcosA}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{2A}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}−\mathrm{sin}^{\mathrm{2}} \mathrm{2A} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}+\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{2A} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{2A} \\ $$$$\therefore\mathrm{1}+\mathrm{cos2A}=\mathrm{2}\left(\mathrm{cos}^{\mathrm{4}} \mathrm{A}+\mathrm{sin}^{\mathrm{4}} \mathrm{A}\right)\:\left(\mathrm{PROVE}\right) \\ $$$$ \\ $$$$ \\ $$
Answered by ridwan balatif last updated on 10/Oct/16
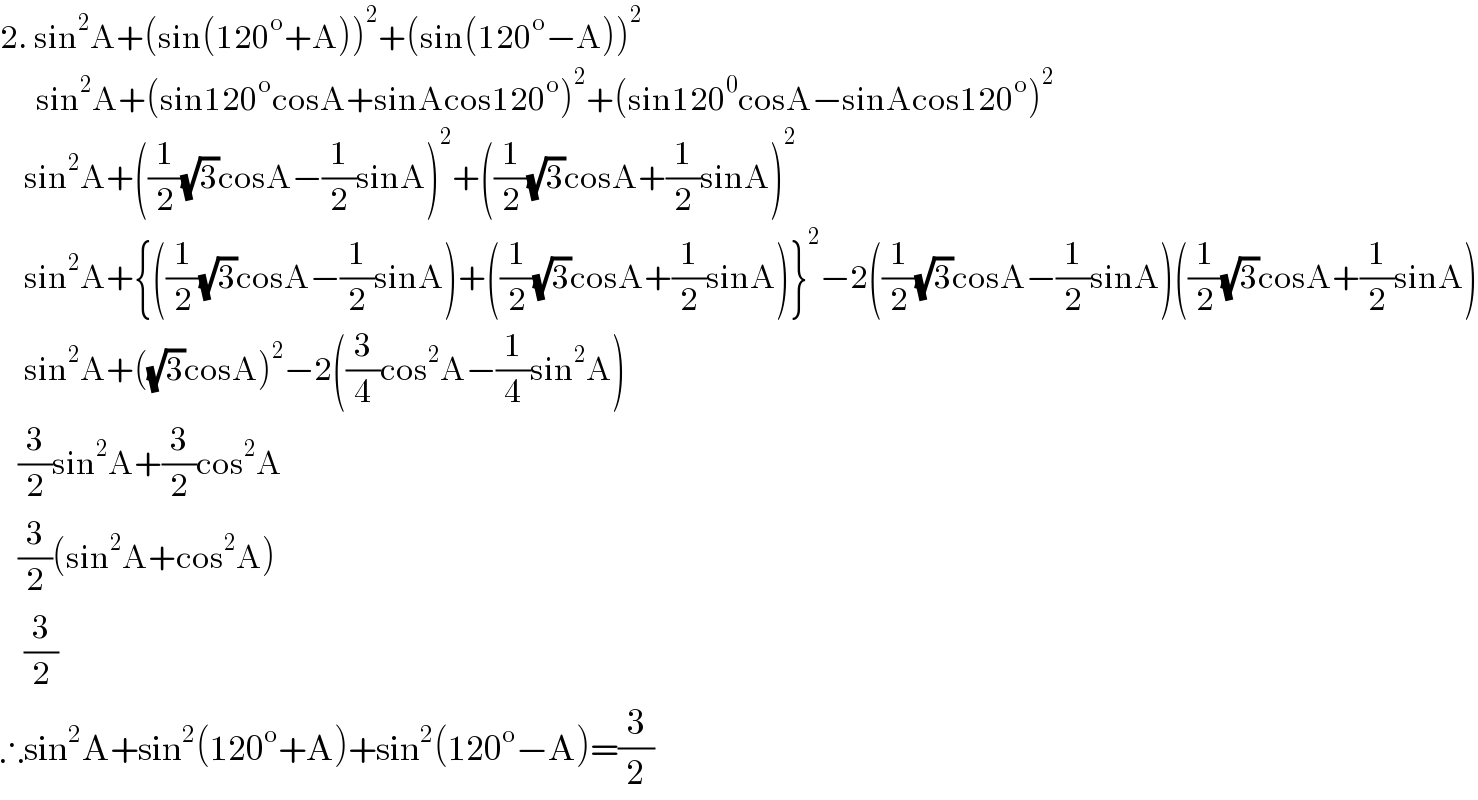
2. sin^2 A+(sin(120^o +A))^2 +(sin(120^o −A))^2 sin^2 A+(sin120^o cosA+sinAcos120^o )^2 +(sin120^0 cosA−sinAcos120^o )^2 sin^2 A+((1/2)(√3)cosA−(1/2)sinA)^2 +((1/2)(√3)cosA+(1/2)sinA)^2 sin^2 A+{((1/2)(√3)cosA−(1/2)sinA)+((1/2)(√3)cosA+(1/2)sinA)}^2 −2((1/2)(√3)cosA−(1/2)sinA)((1/2)(√3)cosA+(1/2)sinA) sin^2 A+((√3)cosA)^2 −2((3/4)cos^2 A−(1/4)sin^2 A) (3/2)sin^2 A+(3/2)cos^2 A (3/2)(sin^2 A+cos^2 A) (3/2) ∴sin^2 A+sin^2 (120^o +A)+sin^2 (120^o −A)=(3/2)
$$\mathrm{2}.\:\mathrm{sin}^{\mathrm{2}} \mathrm{A}+\left(\mathrm{sin}\left(\mathrm{120}^{\mathrm{o}} +\mathrm{A}\right)\right)^{\mathrm{2}} +\left(\mathrm{sin}\left(\mathrm{120}^{\mathrm{o}} −\mathrm{A}\right)\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\mathrm{sin}^{\mathrm{2}} \mathrm{A}+\left(\mathrm{sin120}^{\mathrm{o}} \mathrm{cosA}+\mathrm{sinAcos120}^{\mathrm{o}} \right)^{\mathrm{2}} +\left(\mathrm{sin120}^{\mathrm{0}} \mathrm{cosA}−\mathrm{sinAcos120}^{\mathrm{o}} \right)^{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{sin}^{\mathrm{2}} \mathrm{A}+\left(\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}}\mathrm{cosA}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinA}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}}\mathrm{cosA}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinA}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{sin}^{\mathrm{2}} \mathrm{A}+\left\{\left(\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}}\mathrm{cosA}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinA}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}}\mathrm{cosA}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinA}\right)\right\}^{\mathrm{2}} −\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}}\mathrm{cosA}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinA}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}}\mathrm{cosA}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinA}\right) \\ $$$$\:\:\:\:\mathrm{sin}^{\mathrm{2}} \mathrm{A}+\left(\sqrt{\mathrm{3}}\mathrm{cosA}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{4}}\mathrm{cos}^{\mathrm{2}} \mathrm{A}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}^{\mathrm{2}} \mathrm{A}\right) \\ $$$$\:\:\:\frac{\mathrm{3}}{\mathrm{2}}\mathrm{sin}^{\mathrm{2}} \mathrm{A}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{cos}^{\mathrm{2}} \mathrm{A} \\ $$$$\:\:\:\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{sin}^{\mathrm{2}} \mathrm{A}+\mathrm{cos}^{\mathrm{2}} \mathrm{A}\right) \\ $$$$\:\:\:\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\therefore\mathrm{sin}^{\mathrm{2}} \mathrm{A}+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{120}^{\mathrm{o}} +\mathrm{A}\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{120}^{\mathrm{o}} −\mathrm{A}\right)=\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *