Question Number 8403 by rhm last updated on 10/Oct/16
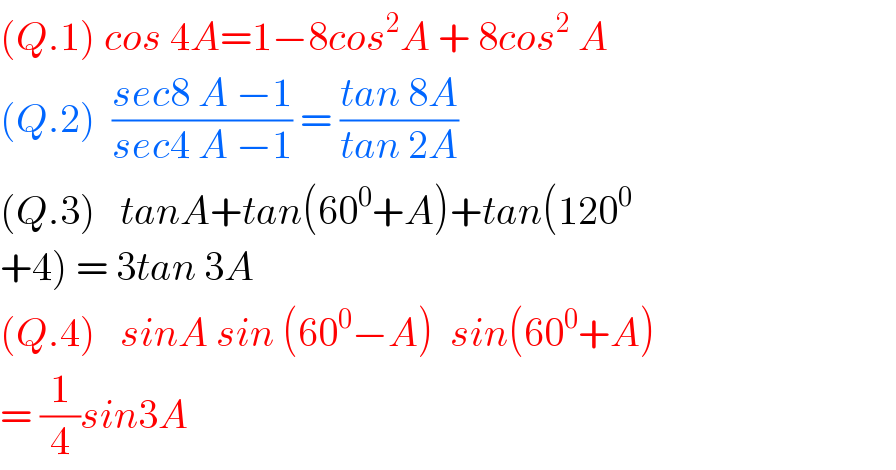
$$\left({Q}.\mathrm{1}\right)\:{cos}\:\mathrm{4}{A}=\mathrm{1}−\mathrm{8}{cos}^{\mathrm{2}} {A}\:+\:\mathrm{8}{cos}^{\mathrm{2}} \:{A} \\ $$$$\left({Q}.\mathrm{2}\right)\:\:\frac{{sec}\mathrm{8}\:{A}\:−\mathrm{1}}{{sec}\mathrm{4}\:{A}\:−\mathrm{1}}\:=\:\frac{{tan}\:\mathrm{8}{A}}{{tan}\:\mathrm{2}{A}} \\ $$$$\left({Q}.\mathrm{3}\right)\:\:\:{tanA}+{tan}\left(\mathrm{60}^{\mathrm{0}} +{A}\right)+{tan}\left(\mathrm{120}^{\mathrm{0}} \right. \\ $$$$\left.+\mathrm{4}\right)\:=\:\mathrm{3}{tan}\:\mathrm{3}{A}\: \\ $$$$\left({Q}.\mathrm{4}\right)\:\:\:{sinA}\:{sin}\:\left(\mathrm{60}^{\mathrm{0}} −{A}\right)\:\:{sin}\left(\mathrm{60}^{\mathrm{0}} +{A}\right)\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}{sin}\mathrm{3}{A} \\ $$
Answered by ridwan balatif last updated on 10/Oct/16

$$\left(\mathrm{Q}.\mathrm{4}\right)\:\mathrm{sinA}.\left(\mathrm{sin}\left(\mathrm{60}^{\mathrm{o}} −\mathrm{A}\right)\mathrm{sin}\left(\mathrm{60}^{\mathrm{o}} +\mathrm{A}\right)\right)\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{sinA}.\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\left(−\mathrm{2A}\right)−\mathrm{cos}\left(\mathrm{120}\right)\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinA}\left(\mathrm{cos2A}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinAcos2A}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sinA} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sin3A}+\mathrm{sin}\left(−\mathrm{A}\right)\right)\right)+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sinA} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin3A}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sinA}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sinA} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin3A}\: \\ $$$$\therefore\mathrm{sinAsin}\left(\mathrm{60}^{\mathrm{o}} −\mathrm{A}\right)\mathrm{sin}\left(\mathrm{60}^{\mathrm{o}} +\mathrm{A}\right)=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin3A}\left(\mathrm{PROVE}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by sandy_suhendra last updated on 10/Oct/16

$$\left(\mathrm{Q}.\mathrm{1}\right)\:\mathrm{I}\:\mathrm{think}\:\mathrm{cos}\:\mathrm{4A}=\mathrm{1}−\mathrm{8cos}^{\mathrm{2}} \mathrm{A}+\mathrm{8cos}^{\mathrm{4}} \mathrm{A} \\ $$$$\mathrm{cos4A}=\mathrm{2cos}^{\mathrm{2}} \mathrm{2A}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left(\mathrm{2cos}^{\mathrm{2}} \mathrm{A}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left(\mathrm{4cos}^{\mathrm{4}} \mathrm{A}−\mathrm{4cos}^{\mathrm{2}} \mathrm{A}+\mathrm{1}\right)−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{8cos}^{\mathrm{4}} \mathrm{A}−\mathrm{8cos}^{\mathrm{2}} \mathrm{A}+\mathrm{2}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}−\mathrm{8cos}^{\mathrm{2}} \mathrm{A}+\mathrm{8cos}^{\mathrm{4}} \mathrm{A} \\ $$
Commented by rhm last updated on 11/Oct/16

$${yes}\:{yov}\:{are}\:{right} \\ $$
Answered by sandy_suhendra last updated on 10/Oct/16

$$\left(\mathrm{Q}.\mathrm{2}\right)\:\frac{\mathrm{sec8A}−\mathrm{1}}{\mathrm{sec4A}−\mathrm{1}}×\frac{\mathrm{cos8A}\:\mathrm{cos4A}}{\mathrm{cos8A}\:\mathrm{cos4A}} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{cos4A}−\mathrm{cos8A}\:\mathrm{cos4A}}{\mathrm{cos8A}−\mathrm{cos8A}\:\mathrm{cos4A}} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{cos4A}\left(\mathrm{1}−\mathrm{cos8A}\right)}{\mathrm{cos8A}\left(\mathrm{1}−\mathrm{cos4A}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{cos4A}\left(\mathrm{2sin}^{\mathrm{2}} \mathrm{4A}\right)}{\mathrm{cos8A}\left(\mathrm{2sin}^{\mathrm{2}} \mathrm{2A}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\left(\mathrm{cos4A}\:\mathrm{sin4A}\right)\:\left(\mathrm{sin4A}\right)}{\mathrm{cos8A}\:\mathrm{sin}^{\mathrm{2}} \mathrm{2A}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin8A}\:\left(\mathrm{2sin2Acos2A}\right)}{\mathrm{cos8A}\:\mathrm{sin}^{\mathrm{2}} \mathrm{2A}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{sin8A}\:\mathrm{cos2A}}{\mathrm{cos8A}\:\mathrm{sin2A}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{tan8A}\:\mathrm{cot}\:\mathrm{2A} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{tan8A}}{\mathrm{tan2A}} \\ $$
